Hello,
I'm not fluently in english, but I gave a french link where I explained the device in french if it's necessary.
I would like to study this device:

The support (a torus, blue color) turns counterclockwise around the center of rotation C1. The center C1 is fixed to the ground.
A red object with compressible balls and springs turns counterclockwise around the center of rotation C2. The center C2 is fixed to the support. The red object
can turn around C2, I drawn the red object above the torus but it's for understand there are 2 objects.
The torus pass throught the red object and balls pressure the right wall of the red object and a part of the "circle" of the torus.

In a part of the red object there are a lot a small balls. Each ball is attracked by a spring (there are a lot of springs). I suppose the balls small like the molecules of water in theory, just for simplify the study. Like that I can apply the law of pressure. The springs act like the gravity can do, it's just for have a pressure to the right wall (I need it).

So, I will have a pressure at right and forces from this pressure, like water can do in a recipient under gravity. The forces from the springs are more and more higher too but a little less because there is the presence of the torus.
Like this the device is very unstable. But I accelerate more and more the support for have : Angular_velocity_of_the_support = Angular_velocity_of_the_red_object. At each time, the support must have the exact angular velocity of the object, it's difficult to do in practise but it's possible and I would like to study the device like that.
Now, I study the sum of momentums and the sum of forces. My goal is to have a torque on the red object but cancel the torque on the support. And it's possible with good values of the force Fx.
The device with distances and datas:

I want to have the sum of forces on the red object in the direction of (C1,C2):

**************************************************************************Calculations*********************************************************************
R=6.5 external radius of the torus
c=3 side of red object where there is balls
d=4.34 distance C1C2 (x or y)
The distance d is obtain with the equation
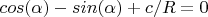
, in this case

I suppose the force of pressure is equal to the height of the balls, it's possible because I can choose the force of the spring. Each spring attrack with same force. I did not give the unity but if it's necessary, it's meter for the distance, Newton for the force, Nm for the momentum.
******************************************Springs**************************************
The start of integration (x):
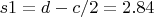
The middle of the integration (x):
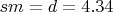
The end of the integation (x):
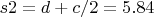
The height:
 Momentums:
Momentums:Integrate1:
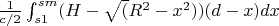
Integrate2:
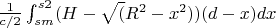
Value:
 Sum of forces:
Sum of forces: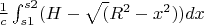
Value:
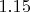
******************************************Side Wall**************************************
Momentums: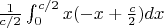
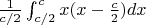
Value:
 Sum of forces:
Sum of forces:Value:
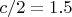
******************************************Left Wall**************************************
I want to cancel of torque on the support, so I need
 Momentums:
Momentums: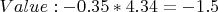
******************************************The Torus************************************
The part of the circle that is in contact with balls don't give a torque to the torus because it's a circle. With Fx the sum of forces on the red object is in the direction of (C1,C2), so there is no torque.
*****************************************Results****************************************
Like that the sum of momentum on the red object is :
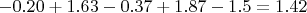
There is no torque on the support. Now, if I accelerated the support like the object, I can keep constant the relative position of the object on the support. It's like the support and the object are fixed together, but there are not ! I need to give an energy for accelerate more and more the support but this energy can be recover later. In the contrary I don't gave any energy for accelerate the red object.
So the device increases its potential energy alone ? Where I'm wrong ?
If it's not clear, I'm asking the question in french here:
http://www.chercheursduvrai.fr/forum/in ... topic=2021


