Построения Гюйгенса для анизотропных кристаллов

[LarisaK]

Здравствуйте уважаемые участники форума. Помогите, плз, найти ошибку в моих рассуждениях. Задачка простенькая, из теста

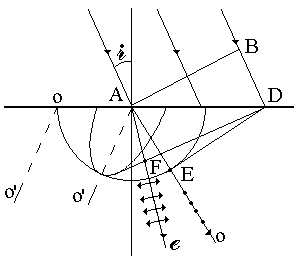
На рисунке выполнено построение Гюйгенса для анизотропного кристалла с использованием сечений лучевых поверхностей. OO' - оптическая ось. Длина отрезка АВ - 1. Выберите правильную совокупность утверждений
1) Кристалл положительный. Луч 1 - обыкновенный.
2) Кристалл отрицательный. Луч 2 - необыкновенный.
3) Кристалл положительный. Луч 1 - необыкновенный.
4) Кристалл отрицательный. Луч 2 - обыкновенный.
5) Построение выполнено неверно.
6) Среди ответов правильного нет.

по ответам правильный вариант 5 (построение выполнено неверно).
А у меня получается 3-ий вариант (Кристалл положительный. Луч 1 - необыкновенный.)
Рассуждалка:
эллипс внутри – это положительный кристалл. Волновая поверхность должна состоять из полусферы (для обыкновенного луча) и и половинки эллипса(для необыкновенного), то есть 1 – это необыкновенный луч (проходит через точку касания эллипса), 2 – обыкновенный (проходит через точку касаниясферы). Выбираем ответ 3. В чем ошибка?

В инете нашла такую же задачку, там построение другое

но я не понимаю, как в этом случае находится точка F, разве она не должна совпадать с точкой касания эллипса?

Спасибо за помощь

[Xey]

По моему вы правы.
А в кристалле необыкновенный распространяется не по нормали к волновому фронту. Волновой фронт движется и по нормали , и соскальзывает в поперечном направлении. Поэтому при падении луча под прямым углом , в кристалле он отклоняется.

[Red_Herring]

Лучевые поверхности для 3хосных кристаллов подробно разобраны в книге Р.Куранта "УЧП" 60х годов стр. 598 (там есть кристаллоптика и магнитная гидродинамика). Поверхность имеет вид весьма сложный; самый интересных эффект—коническая рефракция.

Поверхность нормалей описывается
\begin{align} &\sum_{i=1}^3 \frac{\xi_i^2}{\rho^2-\sigma_i}=1, \qquad \rho^2=\xi_1^2+\xi_2^2+\xi_3^2 \tag{10}\\ \intertext{и поверхность взаимных нормалей—аналогичным уравнением } &\sum_{i=1}^3 \frac{\xi_i^2}{1-\sigma_i\rho^2}=1. \tag{11}\end{align}

Сечения поверхностей см на стр 601

[it12345]

Луча 1 в природе быть не может. Он соответствует коэффициенту преломления, бОльшему бесконечности.
5) Построение выполнено неверно.

[amon]

it12345 в сообщении #1041949 писал(а):

Луча 1 в природе быть не может.

Гуглим "отрицательный показатель преломления".

[it12345]

В задаче сказано: "кристалл". А не "метаматериал".

[amon]

Плохо гуглили.

[it12345]

LarisaK в сообщении #1041278 писал(а):

но я не понимаю, как в этом случае находится точка F, разве она не должна совпадать с точкой касания эллипса?

Самое интересное, что в комментариях к этому рисунку (рис.9) здесь:
http://works.tarefer.ru/89/100386/index.html
написано: "линии, соединяющие точку A с точками касания сферической и эллипсоидальной поверхностей с касательными DF и DE, дают соответственно необыкновенный и обыкновенный лучи".

И есть аналогичная картинка построения для отрицательного кристалла, на котором всё чики-пуки (рис.5):
http://genphys.phys.msu.ru/mitin/Seminar/Optika_8Anizotrop.pdf

Может быть, при таком расположения падающего луча относительно
оптической оси необыкновенного луча вовсе нет? Может быть, если мы на кристалл посветим лазером под таким углом к оптической оси - то мы вовсе не увидим необыкновенного луча? Как мне кажется, в определённых направлениях раздваивания изображения, наблюдаемого через, например, одноосный кристалл, нет. И причём это не только направление, совпадающее с оптической осью.

[Red_Herring]

it12345 в сообщении #1042105 писал(а):

И причём это не только направление, совпадающее с оптической осью.

И все ортогональные к нему

[it12345]

Red_Herring писал(а):

И все ортогональные к нему

С чего бы это вдруг?
Вроде бы в направлениях, ортогональных оптической оси, скорость обыкновенного и необыкновенного луча не просто разная, а максимально разная.

[Red_Herring]

it12345 в сообщении #1042159 писал(а):

не просто разная, а максимально разная.

Но--одинаковонаправленные

Впрочем, все разговоры об обыкновенных и необыкновенных лучах похоже основаны на абсолютно неверном предположении, что поверхность лучей это два эллипсоида

[Xey]

it12345 в сообщении #1041949 писал(а):

Луча 1 в природе быть не может. Он соответствует коэффициенту преломления, бОльшему бесконечности.
5) Построение выполнено неверно.

Нет, такой ход необыкновенного возможен.
При нормальном падении на кристаллическую пластинку (угол падения 0), необыкновенный луч может идти в пластине под углом, а выходить параллельно падающему.

[Xey]

Если бы луч падал чуть слева, то необыкновенный оставался бы слева от нормали. Чего не бывает для обыкновенного луча (если не метаматериал)


http://don.on.ufanet.ru/5.html

[it12345]

Так казалось бы - а зачем тогда метаматериалы изобретать?
Нельзя просто использовать необыкновенный луч в определённым образом вырезанном положительном кристалле?