Я продолжу здесь.
Я стараюсь взять то, что мне подходит из доказательства Теоремы 1 из этой статьи:
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=tdm&paperid=44&option_lang=rus(Только у меня не конечная группа, а целые числа).
Пусть у меня есть две дискретные цепи Маркова
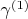
и

; Суммарная цепь

, где

.
Тогда, согласно теореме 6.3.2 у Кемени, Спелл ("Конечные цепи Маркова") об укрупнении состояний марковской цепи,

будет цепью Маркова тогда и только тогда, когда

Для любых

- пространства состояний новой цепи

,

- ее переходные вероятности.
Уравнения Колмогорова-Чепмена(?) позволяют переписать это в виде:
Для любых фиксированных

справедливы равенства

Где суммирование проводится по всем

;

-вероятности перехода соответствующих цепей.
Я беру самый простой приходящий на ум пример суммы двух цепей, являющихся суммами независимых случайных величин с распределением

, и расписать вероятность

для цепи

:
Пусть

, зафиксируем

и расписываем вероятность перехода, ненулевые слагаемые


Выходит так: в общем случае, программа для каждой вероятности

должна перебрать для каждого разложения

все другие его разложения

(можно разделить на 2 благодаря симметричности), и в каждом случае этих разложений - все разложения

. (Невесело).
Буду очень благодарен за любые советы и комментарии. Хотелось бы придумать пару красивых примеров хотя бы.



