Последовательность

имеет конечный предел
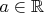
Доказать, что

Задача в общем не сложная, в том смысле что результат и метод какой ожидаются понятен. Но я не понимаю как сделать один переход, проясните, пожалуйста.
1. Запишем определение предела для последовательности


2. В предложенных обозначениях


3. Но раз выполнено для всех таких

, то будет лежать в их пересечении, поэтому:

Дальше мне понятно, что будет

-- опять же раз для всех, то лежит в пересечении, и как раз таким образом зажмем множество только до предельной точки

. А как "существует" и объединение связаны мне не ясно.