Насчет спутника не уверен.
Описание очень похоже.
Он бы не стал менять яркость,
Реальные спутники это отлично делают - за счет входа/выхода в тень Земли, собственного вращения, разной воздушной массы на луче зрения и т.д.
а также ускоряться и замедляться
Ну уж...

Хотя это отчасти психологический эффект - яркий объект кажется движущимся быстрее, чем тусклый - но и скорость тоже меняется. Только не линейная, а угловая, и именно по отношению к Вам.
Давайте сделаем простенькую модель. Вы сидите на поверхности Земли, над Вами пролетает низкоорбитальный спутник (пусть для определенности он летает на высоте

над поверхностью), для простоты будем считать, что пролетает он через зенит, причем в момент

. Если угловая скорость спутника относительно центра Земли

, то угол при центре Земли в треугольнике Вы-центр Земли-спутник в некоторый момент

будет равен

. Тогда угол

при спутнике можно получить из такого соотношения

где

- радиус Земли,

- расстояние от Вас до спутника.
Наблюдаемая угловая скорость спутника

будет отношением тангенциальной скорости

и расстояния до него

:

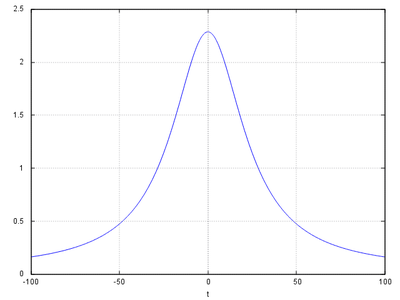
Если для данных выше нарисовать график

, получится нечто такое:
Вложение:
 sat.png [ 16.41 Кб | Просмотров: 0 ]
sat.png [ 16.41 Кб | Просмотров: 0 ]
По оси абсцисс время в секундах, по оси ординат - угловая скорость в градусах в секунду.
В зените скорость максимальна, на "краях" - заметно меньше. При других параметрах количественно результат "поедет", но качественно будет выглядеть так же.
-- 27.06.2015, 01:08 -- Я видел и сгорающие быстро и те, которые двигались довольно медленно и долго. Мне кажется это должно зависеть от траектории, под каким прицельным углом метеор налетает на Землю, может влететь так, что быстро достигнет плотных слоёв атмосферы и сразу сгорит, может долго спускаться.
В первую очередь это зависит от массы метеорного тела. Но, скорее всего, то, что Вы видели летящим "медленно и долго", тоже было ИСЗ - крупные болиды редко кому удается увидеть чаще одного раза в жизни.
 -- 27.06.2015, 01:17 --
-- 27.06.2015, 01:17 --Он бы не стал менять яркость,
Да, кстати, до кучи уж... Наш модельный спутник, летающий на высоте 200 км, проведет над горизонтом наблюдателя (т.е.Вас) несколько больше 6 минут. При этом создаваемая им освещенность в зените и на горизонте (между этими двумя положениями, соответственно, пройдет чуть больше 3 минут) изменится примерно в тысячу раз только за счет разной толщины слоя воздуха, находящегося между ним и Вами. Так что уже одного этого обстоятельства более чем достаточно для того, чтобы спутник сначала "разгорелся", а потом "потух".



