Представьте себе вращающийся цилиндр. Однако цилиндр вращается не только вокруг своей оси, но и вокруг прямой, которая проходит перпендикулярно плоскости, на которой находиться цилиндр. Наглядно это показано на рисунке.
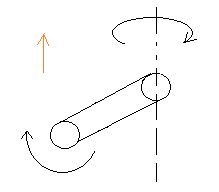
Как вычислить подъёмную силу цилиндра возникающую из-за эффекта Магнуса? Если бы вращающийся цилиндр двигался бы прямолинейно, то вычислить подъёмную силу можно было бы легко по формуле

, где

-радиус цилиндра,

-его длина,

-плотность среды в которой он находиться,

-число его оборотов,

-скорость набегающего потока. А в случае двухмерного вращения скорость набегающего потока воздуха можно узнать проинтегрировав эту скорость по длине цилиндра. Скорость набегающего потока можно определить как функцию от длины цилиндра

, где

- число оборотов цилиндра во время вращения в плоскости,

- длина цилиндра.
Проинтегрировав эту функцию получим

Итак, подъёмная сила цилиндра для случая двухмерного вращения равна

Верно ли это?