Добрый день!
Пытаюсь самостоятельно изучать ТАУ - в частности, уравнения состояния системы. Обнаружил более-менее понятную книгу по адресу:
https://en.wikibooks.org/wiki/Control_S ... _SolutionsТам приводится решение уравнения состояния системы с ненулевым входом:

Это уравнение домножается на
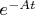
(с переносом

влево) - и получается так:

А потом то, что слева, преобразуется по формуле производной от произведения функций:

Далее это уравнение решается со следующими пояснениями:
Цитата:
Now we can integrate both sides, from the initial time (

) to the current time (

), using a dummy variable

, we will get closer to our result. Finally, if we premultiply by

, we get our final result:
"Теперь мы можем интегрировать обе стороны, от начального времени(

) до текущего времени(

), используя вспомогательную переменную

, мы подойдём ближе к нашему результату. В конце концов, если мы предварительно умножим на

, то мы получим наш окончательный результат:

Так вот я и не могу понять, как интегрируется и решается это уравнение. Может быть, кому-нибудь будет несложно восстановить промежуточные шаги - или ткнуть пальцем, где этот процесс разжёван и в рот положен, чтобы осталось только проглотить?



