Добрый день, пожалуйста, помогите разобраться
необходимо доказать

, используя теорему Чевы
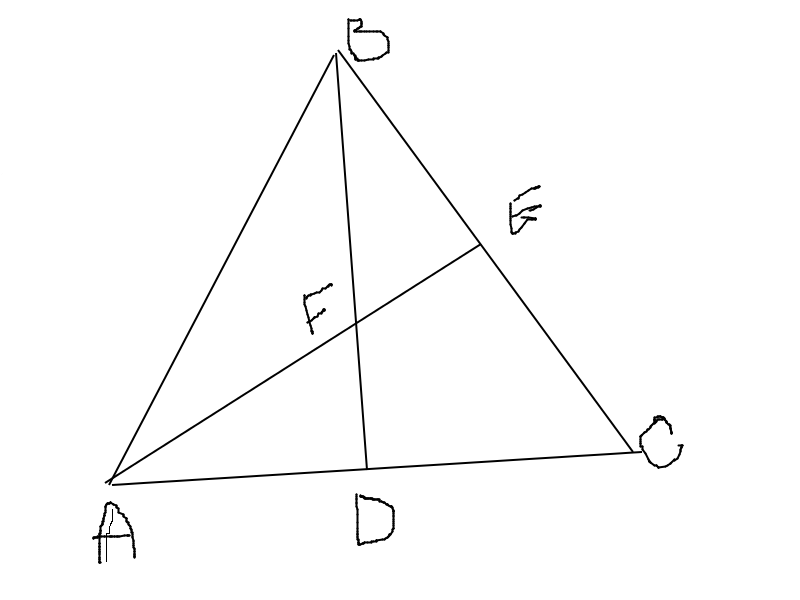
Мой вариант :
К сожалению ничего неизвестно о расположении точек на сторонах. Я предлогожил, что они образуют медианы
Поделим все выражение на

Получится

Если все же считать АЕ медианой, то очевидно

, тогда

= 2
Далее используем теорему Менелая (она как-то свазана с теоемой Чева):
Отсюда левая честь будет равна

получаем, что BC в 2 раза большее ВЕ (т.е

)
Вернемся обратно



Но если точки все же произвольные, то решить не смогу
Спасибо!