А если вы думаете, что коэффициенты Тейлора в этой задаче находятся также как и в теореме Коши-Ковалевской, то вы просто не в теме.
Поскольку уравнение разрешено относительно старшей производной по

, то алгоритм нахождения коэффициентов точно такой же, как и в теореме КК. Что не получается—так это разрешимость в классе функций аналитических по

, приходится предполагать "супераналитичность":

где

это количество производных по

которых "стоит" одна производная по

(в данной задаче
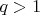
).
PS. Впрочем, бывает и в другую сторону: если ур-е

(к примеру), то

и получается класс Жевре с показателем

. Разумеется, эти ограничения налагаются не только на начальные данные и правую часть, но и коэффициенты ур-ния.
PPS. Разумеется, мы говорим о
единственности в классе аналитических функций. Если отказаться от условия аналитичности (и условий на бесконечности), то даже для УТ

единственности нет.
PPPS. Разумеется бывают и ур-ния, у которых старшая производная по

"обременена" (коэффициентом ли просто, оператором ли): например у-ние

описывающее ур-ние малых колебаний вращающейся жидкости. Там, действительно, даже с единственностью в классе аналитических функций все не так просто.