Здравствуйте.
Подскажите, пожалуйста, почему, если

- независимые одинаково распределённые случайные величины, то
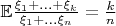
. (E - мат. ожидание).
Про с. в. ничего больше неизвестно (существование у них самих мат. ожидания или т. п.)
Совершенно не имею представления, как это решать. Мне это непонятно ни в одном частном случае (простые с. в, две с. в. и т. д.).
Тут же нельзя просто делить... а как тогда... Непонятно.
Может, я не вижу какой-то очевидности.
Подскажите, пожалуйста.
Заранее спасибо.