Аксиоматика Пеано ничего не даёт для объяснения логических связок, более того сама использует логические связки.
А это не обычная арифметика, а формализованная. Обычная формулируется на естественном языке и понимается в меру распущености. (

)
Не любая запись с буквами, скобками и логическими связками имеет смысл. Поэтому прежде, чем производить какие-то действия, нужно определиться что вообще такое буквы, скобки, логические связки, алфавит...
О Диэдр, но это-то вообще сама простота! Только я для своей простоты буду вместо чисел использовать бинарные строки. Нам нужно закодировать символы

(переменные будут

) и функциональные и предикатные символы теории (для теории множеств, понятно, один только

). Кстати, тут полезно бы использовать польскую нотацию (скобки выкидываем), индексы де Брёйна (выкидываем связанные переменные и некорректные подстановки) и прочие упрощающие жизнь штучки.
Итак, символов получилось 13 (это знак, знак!). Значит, каждый из них будем кодировать четырьмя нулями-единицами. Пускай, например, коды будут соответственно 0001—1101. Кодом строки в нашем алфавите будет строка длины
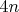
, каждая последовательная четвёрка цифр которой равны коду какого-то символа. Дальше мы можем выразить конкатенацию строк через конкатенацию строк (удивительно), выразить всякие подстановки, проверку на то, является ли строка формулой, есть ли в формуле подформула и т. п.. Потом станем кодировать последовательности формул как строки, в которых отдельные формулы разделены, скажем, последовательностью 0000. Теперь можно выразить, является ли последовательность выводом и другие вещи.
Я просто не знаю, на что дать ссылку (ну не на
GEBaEGB Хофштадтера же, там для нематематиков), а так это кусок конспекта того, что есть в книгах с классическим доказательством теорем Гёделя о неполноте.
-- Вт май 26, 2015 17:07:03 --что есть в книгах
Но там обычно арифметика, но не составит труда сопоставить последовательности натуральным числам. Хотя бы просто добавляем к последовательности слева единицу и рассматриваем результат как представление в двоичной системе. Соотношения

выразить удастся (

— это пустая строка).



