Предлагаю обсудить найденное мной общее решение системы уравнений ОТО для Мира с плоским пространственным сечением с учётом лямбда члена и идеальной пыли.
Решения Шварцшильда, Фридмана и де Ситтера и все их комбинации друг с другом являются частными случаями общего решения.
Уравнения.Ищем решение уравнений ОТО с лямбда членом

и Фридмановской идеальной пылью в правой части:

Метрика сферически симметрична и зависит всего от одной функции

:

Отличные от нуля компоненты тензора Эйнштейна:





Точкой и штрихом обозначено дифференцирование по

и по

соответственно.
Поскольку идеальная пыль не имеет Лагранжиана её учёт осуществляется следующим образом. Сначала решаются "

", "

", "

" и "

" уравнения. Для них правая часть равна нулю. То что получилось для левой части "

" уравнения объявляется плотностью энергии идеальной пыли.
Легко видеть, что "

", "

", "

", "

" уравнения сводятся всего к одному уравнению:
 Общее решение.
Общее решение.Общее решение для

можно записать в неявном виде:

Здесь

-- произвольная функция двух переменных. Случаю
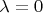
соответствует

Далее рассмотрены частные случаи.
Решение Шварцшильда.Выбор

и устремление лямбда члена к нулю в результате даёт

что соответствует решению Шварцшильда в системе координат Пэнлевэ. Если не устремлять лямбда член к нулю, то получается
 Решение Фридмана.
Решение Фридмана.Выбор

и устремление лямбда члена к нулю в результате даёт

что соответствует решению Фридмана. Сделав преобразование координат его можно привести к каноническому виду:

Если не устремлять лямбда член к нулю, то получается
 Решение де Ситтера.
Решение де Ситтера.Выбор

даёт

что соответствует решению де Ситтера. Сделав преобразования координат его можно привести к одному из канонических видов:

 Комбинация решений Шварцшильда и де Ситтера.
Комбинация решений Шварцшильда и де Ситтера.Выбор

даёт

что соответствует чёрной/белой дыре в пространстве де Ситтера. Сделав преобразование координат его можно привести к каноническому виду:
 Комбинация решений Шварцшильда и Фридмана.
Комбинация решений Шварцшильда и Фридмана.Выбор

и устремление лямбда члена к нулю даёт

что при

переходит в решение Шварцшильда с переменной массой, а при

переходит в решение Фридмана. Если не устремлять лямда член к нулю, то получается
 Комбинация решений Фридмана и де Ситтера.
Комбинация решений Фридмана и де Ситтера.Выбор

даёт

При

это решение переходит в решение де Ситтера, а при

и равном нулю лямбда члене оно переходит в решение Фридмана.
Всем желающим предлагаю рассмотреть более сложные

и получить свои варианты смеси решений Шварцшильда, Фридмана и де Ситтера.