
. Если предположить (что естественно, но не очевидно!), что норма матрицы не меняется при транспонировании, то проходит предыдущее рассуждение, доказывающее, что норма не может быть меньше 1.
, спасибо, по-моему, это то, что нужно. Доказать равенство нормы матрицы
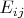
и ее транспонированной можно с помощью преобразования подобия. Подберем невырожденную матрицу

такую, что

. Тогда по свойству нормы получаем

. Аналогично доказываем, что

.
-- Вт май 19, 2015 19:56:29 --А для

можно построить норму, сколь угодно близкую к 0, так как других собственных чисел нет. Документ по моей ссылке посмотрите все-таки.
, вариант со спектральным радиусом здесь, по-моему, не работает. В схеме доказательства, предложенной
Bruklovod, вроде бы, все верно и мультипликативная норма матриц
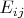
не может быть меньше

. В любом случае, спасибо за ссылку, на досуге почитаю, возможно найду для себя что-то полезное.