Последовательность. Аля-Фиббоначи;)

[mr.tumkan]

Последовательность $a_1,a_2,...,a_n$ состоит из натуральных чисел, причем $a_{n+2}=a_{n+1}+a_n$, $n\in \mathbb{N}$

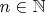
a) Может ли выполняться равенство $4a_5=7a_4$?

b) Может ли выполняться равенство $5a_5=7a_4$?

c) При каком наибольшем натуральном $n$ может выполняться равенство $\dfrac{a_{n+1}}{a_n}=\dfrac{n^2+24}{6n}$

Первые два пункта понятны. $a_3=a_2+a_1$, $a_4=a_3+a_2=2a_2+a_1$, $a_5=a_4+a_3=2a_2+a_1+a_2+a_1=3a_2+2a_1$

a) $4a_5=7a_4$, то есть $4(3a_2+2a_1)=7(2a_2+a_1)$, то есть $12a_2+8a_1=14a_2+7a_1$, тогда $a_1=2a_2$

Возьмем $a_2=1$, тогда получаем последовательность $2;1;3;4;7$, проверка: $4\cdot 7=7\cdot 4$.

b) $5a_5=7a_4$, то есть $5(3a_2+2a_1)=7(2a_2+a_1)$, то есть $15a_2+10a_1=14a_2+7a_1$, тогда $a_2=-3a_2$

Получаем противоречие, потому как члены последовательности положительны. Значит не может выполняться равенство.

c) $\dfrac{a_{n+1}}{a_n}=\dfrac{n^2+24}{6n}$

Так как последовательность возрастает, получаем, что $\dfrac{n^2+24}{6n}>1$, то есть $n^2-6n+24>0$, что выполняется при всех натуральных $n$.

За что здесь можно зацепиться, как дальше в пункте $c)$ ???

[mihailm]

Ну докажите, для начала, что $\dfrac{a_{n+1}}{a_n}$ при $n>1$ не больше двух.

[mr.tumkan]

mihailm в сообщении #1013536 писал(а):

Ну докажите, для начала, что $\dfrac{a_{n+1}}{a_n}$ при $n>1$ не больше двух.

$a_{n+2}=a_{n+1}+a_n<a_n+a_n=2a_n$

Тогда $\dfrac{a_{n+1}}{a_n}<2$

[mihailm]

ну вот уже какое-то ограничение на $n$, хотя доказательство и не совсем

[mr.tumkan]

$\dfrac{n^2+24}{6n}<2$

$n^2-12n+24<0$

$(n-6)^2<12$

$-2\sqrt{3}<n-6<2\sqrt{3}$

$6-2\sqrt{3}<n<2\sqrt{3}+6$

Значит $n\leqslant 9$

Но это пока что оценка. Не уж-то нужно в лоб подбирать? Есть ли способ проще?

[mihailm]

Теперь попробуйте двойку уменьшить

[mihailm]

(Оффтоп)

Чисто позанудствовать: Аля-Фиббоначи очень неудачная конструкция, лучше А-ля Фибоначчи или А ля Фибоначчи

[svv]

А в лоб подобрать тоже нетрудно. Пусть $n=7$ (например). Тогда $\frac{a_8}{a_7}=\frac{73}{42}$. Так мы можем взять $a_8=73$, $a_7=42$, а дальше, пользуясь $a_{n+2}-a_{n+1}=a_n$, найти $a_6=31$, $a_5=11$, $a_4=20$, $a_3=-9$ (приехали!). Потому что любая другая аля-последовательность с тем же отношением $\frac{a_8}{a_7}$ отличается от нашей лишь на общий положительный множитель и тоже на $a_3$ вылетит в отрицательную область.

[arseniiv]

(Оффтоп)

mihailm в сообщении #1013605 писал(а):

Чисто позанудствовать: Аля-Фиббоначи очень неудачная конструкция, лучше А-ля Фибоначчи или А ля Фибоначчи

Une suite à la Fibonacci.

[mr.tumkan]

Что-то двойку не получается уменьшить

-- 12.05.2015, 14:22 --

Только там была опечатка:

$a_{n+2}=a_{n+1}+a_n<a_{n+1}+a_{n+1}=2a_{n+1}$

Тогда $\dfrac{a_{n+1}}{a_n}<2$

[mihailm]

mr.tumkan в сообщении #1013845 писал(а):

Что-то двойку не получается уменьшить...

надо не два предыдущих слагаемых брать, а больше.
Но на самом деле можно обойтись и без этого. $n=9$ подойдет?

[mr.tumkan]

mihailm в сообщении #1014045 писал(а):

mr.tumkan в сообщении #1013845 писал(а):

Что-то двойку не получается уменьшить...

надо не два предыдущих слагаемых брать, а больше.
Но на самом деле можно обойтись и без этого. $n=9$ подойдет?

Нет, не подойдет, подойдет $n=5$. Но это утомительно очень перебирать варианты. А как все-таки можно улучшить оценку, я взял более двух слагаемых, что-то не помогло. Нам ведь нужно связать "два соседних" члена, а тут получается, что не соседние, если подключать последующие.