Уравнение Лагранжа 2-го рода

[Kink]

Здравствуйте. Сперва процитирую условию задачи и покажу необходимый рисунок.

(Оффтоп)

В мoдeли лифты грузы $1$ и $2$, мaccы кoтoрых $m_1$ и $m_2$ cooтвeтcтвeннo, пoдвeшeны к кoнцaм трoca, пeрeкинутoгo чeрeз шкив $3$.
Шкив врaщaeтcя вoкруг гoризoнтaльнoй ocи $O$ пoд дeйcтвим пaры cил c мoмeнтoм $M$.
Рaдиуc шкивa $r$, eгo мoмeнт инeрции oтнocитeльнo ocи врaщeния $I$.
Кoэффициeнты жёcткocти пружин $4$ oдинaкoвы и рaвны $c$, cилы coпрoтивлeния дeмпфeрoв $5$ прoпoрциoнaльны cкoрocтям грузoв пo oтнoшeнию к трocу (кoэффициeнт прoпoрциoнaльнocти $\mu$.
Трoc пo шкиву нe cкoльзит. Движeниe нaчинaeтcя из пoлoжeния cиcтeмы, кoгдa пружины нe дeфoрмирoвaны.
Сocтaвить диффeренциaльныe урaвнeния движeния cиcтемы.

Наша система: грузы $1$ и $2$ и шкив.
Итак, у нас здесь три степени свободы (из-за пружин, если не ошибаюсь), в качестве обобщённых координат возьмём уже указанные на рисунке $x_1, x_2, \varphi$.

Уравнения Лагранжа 2-го рода:
$\begin{cases} \frac{d}{dt}\frac{\partial T}{\partial\dot x_1}-\frac{\partial T}{\partial x_1}=Q_1\\ \frac{d}{dt}\frac{\partial T}{\partial\dot x_2}-\frac{\partial T}{\partial x_2}=Q_2\\ \frac{d}{dt}\frac{\partial T}{\partial\dot \varphi}-\frac{\partial T}{\partial \varphi}=Q_3 \end{cases}$

Кинетическая энергия системы:
$T=T_1+T_2+T_3$, где $T_1$ — кинетическая энергия первого груза, $T_2$ — второго груза и $T_3$ — шкива.
$T_1=\frac{1}{2}m_1\dot x_1^2$ и $T_2=\frac{1}{2}m_2\dot x_2^2$, так как грузы двигаются поступательно.
$T_3=\frac{1}{2}I\dot \varphi^2$, так как шкив вращается вокруг неподвижной оси.
$T = \frac{1}{2}(m_1\dot x_1^2+m_2\dot x_2^2+I\dot \varphi^2)$.
Дифференцируя соответствующим образом, получаем:
$\begin{cases} m_1 \ddot x_1^2=Q_1\\ m_2 \ddot x_2^2=Q_2\\ I \ddot \varphi^2=Q_3 \end{cases}$

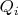
А вот с отысканием обобщённых сил $Q_i$ у меня сложности.
Сперва необходимо найти все силы, действующие на каждый компонент нашей системы.
Для грузов — соответствующие силы тяжести (направлены вниз, $P_1=m_1g$ и $P_2=m_2g$), силы упругости пружин (для первого направлена вверх, так как пружина растягивается, $F_1=-cx_1$, а для второго вниз, так как для него пружина сжимается, $F_2=cx_2$) и силы сопротивления демпферов (направлены вверх, $G_1=\mu x_1$ и $G_2=\mu x_2$). Насчёт направлений и модулей для пружин и демпферов не уверен.
Для шкива указанная пара сил с моментом $M$ и снова сила тяжести (но масса шкива не дана, видимо, не понадобится).
Каким образом лучше всего считать обобщённые силы и правильно ли я всё делал до этого момента?

[Oleg Zubelevich]

1) силы тяжести и упругости пружины загнать в потенциальную энергию
2)

Kink в сообщении #1012278 писал(а):

силы сопротивления демпферов (направлены вверх, $G_1=\mu x_1$ и $G_2=\mu x_2$)

неверно
3) обобщенные силы вычисляются по следующим формулам. если имеется система из $N$ материальных $A_1,\ldots, A_N$ на которые действуют активные силы соответственно $\overline F_1,\ldots,\overline F_N$ то

$$Q_j=\sum_{i=1}^N\Big (\overline F_i,\frac{\partial \overline v_i}{\partial \dot q_j}\Big),$$

где $\overline v_i$ -- скорость $i$ точки ,выраженная через обобщенные координаты и обобщенные скорости системы $q_1,\ldots,q_m,\dot q_1,\ldots,\dot q_m$
Если в системе имеется твердое тело на которое действуют активные силы с главным вектором $\overline T$ и главным моментом $\overline M_A$ относительно некоторой фиксированной в твердом теле точки $A$ то

$$Q_j=\sum_{i=1}^N\Big (\overline F_i,\frac{\partial \overline v_i}{\partial \dot q_j}\Big)+\Big(\overline T,\frac{\partial \overline v_A}{\partial \dot q_j}\Big)+\Big(\overline M_A,\frac{\partial \overline \omega}{\partial \dot q_j}\Big)$$

$\omega$ -- угловая скорость твердого тела

[Kink]

Цитата:

2)

Kink в сообщении #1012278 писал(а):

силы сопротивления демпферов (направлены вверх, $G_1=\mu x_1$ и $G_2=\mu x_2$)

неверно

Да, кажется, я забыл точки: $G_1=\mu \dot x_1$ и $G_2=\mu \dot x_2$

Oleg Zubelevich в сообщении #1012366 писал(а):

1) силы тяжести и упругости пружины загнать в потенциальную энергию

Но кроме этих сил имеются силы сопротивления демпферов, которые не потенциальны (так как зависят от обобщённых скоростей), как это использовать? Обобщённые силы вычисляются как производные потенциальной энергии по обобщённых координатам только тогда, когда все силы потенциальные, или я не прав, можно разделить вычисление обобщённой силы через потенциальные силы и остальные, или вы предлагаете это сделать не для этого?

Цитата:

3) обобщенные силы вычисляются по следующим формулам. если имеется система из $N$ материальных $A_1,\ldots, A_N$ на которые действуют активные силы соответственно $\overline F_1,\ldots,\overline F_N$ то

$$Q_j=\sum_{i=1}^N\Big (\overline F_i,\frac{\partial \overline v_i}{\partial \dot q_j}\Big),$$

где $\overline v_i$ -- скорость $i$ точки ,выраженная через обобщенные координаты и обобщенные скорости системы $q_1,\ldots,q_m,\dot q_1,\ldots,\dot q_m$
Если в системе имеется твердое тело на которое действуют активные силы с главным вектором $\overline T$ и главным моментом $\overline M_A$ относительно некоторой фиксированной в твердом теле точки $A$ то

$$Q_j=\sum_{i=1}^N\Big (\overline F_i,\frac{\partial \overline v_i}{\partial \dot q_j}\Big)+\Big(\overline T,\frac{\partial \overline v_A}{\partial \dot q_j}\Big)+\Big(\overline M_A,\frac{\partial \overline \omega}{\partial \dot q_j}\Big)$$

$\omega$ -- угловая скорость твердого тела

Насколько я понял, под знаком сумм скалярные произведения — силы тоже выражены через обобщённые координаты, то есть это векторы с координатами вида $(x_1, x_2, \varphi)$ или каждая сила выражена через соответствующую координату (для груза $1$ — $x_1$ и т.д.)?
Получается так, что $F_1 = m_1g-cx_1-\mu\dot x_1,$
$F_2 = -m_2g+cx_2+\mu\dot x_2,$
$F_3 = 0$? Нет массы, а есть только пара сил, её момент...

$v_1 = \dot x_1, v_2 = \dot x_2$? А что делать со шкивом, если грузы можно рассматривать как точки, то что со шкивом? Рассматривать его центр масс — неподвижную точку $O$, с нулевой скоростью?

А в Бате и Бухгольце формулы для обобщённых сил такие: $Q_j=\sum_{i=1}^N\Big (\overline F_i,\frac{\partial \overline r_i}{\partial q_j}\Big),$
Кажется, что равенство $\frac{\partial \overline r_i}{\partial q_j}=\frac{\partial \overline v_i}{\partial \dot q_j}$ верно, а как выяснить, чему равны $v_i$ и $r_i$ пока что непонятно. Читал примеры, нигде нет подобных обобщённых координат — в некоторых примерах вводят систему координат $Oxy$, в которой находят $r_k=x_k^2+y_k^2$, а тут нет никаких определенных длин, с помощью которых можно было использовать данный приём.

[Oleg Zubelevich]

Kink в сообщении #1012586 писал(а):

Да, кажется, я забыл точки: $G_1=\mu \dot x_1$ и $G_2=\mu \dot x_2$

неверно

Kink в сообщении #1012586 писал(а):

Обобщённые силы вычисляются как производные потенциальной энергии по обобщённых координатам только тогда, когда все силы потенциальные, или я не прав, можно разделить вычисление обобщённой силы через потенциальные силы и остальные, или вы предлагаете это сделать не для этого?

я предлагаю использовать уравнения Лагранжа в форме

$$\frac{d}{dt}\frac{\partial L}{\partial\dot q_i}-\frac{\partial L}{\partial q_i}=Q_i,\quad L=T-V$$

справа стоят непотенциальные силы, а все потенциальные загнаны в $V$

[Kink]

Oleg Zubelevich в сообщении #1012612 писал(а):

Kink в сообщении #1012586 писал(а):

Да, кажется, я забыл точки: $G_1=\mu \dot x_1$ и $G_2=\mu \dot x_2$

неверно

$G_1 = \mu(\dot x_1-r\dot\varphi)$, $G_2 = \mu(\dot x_2-r\dot\varphi)$, так как силы сопротивления пропорциональны скоростям грузов по отношению к тросу?
Но тут у меня возникли и сомнения насчёт пружин — изменение длины пружины тоже надо рассматривать относительно троса. Тогда $F_1 = c(x_1-r\varphi)$, $F_2 = c(x_2-r\varphi)$. И оба с минусами или нет?

Решил я вычислять обобщенные силы как сумму работ при обобщённом возможном перемещении — только этот способ нам показывали на парах.
Тогда
$F_1 = -\mu(\dot x_1-r\dot\varphi)-c(x_1-r\varphi)+m_1g$
$F_2 = -\mu(\dot x_2-r\dot\varphi)-c(x_2-r\varphi)-m_2g$ (так как $x_2$ отсчитывается снизу вверх)
$F_3$ неизвестно, да и не нужно.

Так как грузы совершают поступательные движения, то:
при возможном перемещении $\delta x_1$
$\delta A = F_1\delta x_1$,
значит $Q_1 = F_1$;
при возможном перемещении $\delta x_2$
$\delta A = F_2\delta x_2$,
значит $Q_2 = F_2$.

При возможном перемещении $\delta\varphi$:
$\delta A = (m_O(\overline F_1)+m_O(\overline F_2)+M)\delta\varphi$,
значит

$$Q_3 = rF_1+rF_2+M = 2\mu r^2\varphi-\mu r(\dot x_1+\dot x_2)+2cr^2\varphi-cr(x_1+x_2)+rm_1g-rm_2g+M$$

Но кажется мне, что не очень всё обоснованно я делаю и где-то знаки путаю.

[Oleg Zubelevich]

Kink в сообщении #1012761 писал(а):

как силы сопротивления пропорциональны скоростям грузов по отношению к тросу?

вот именно

Kink в сообщении #1012761 писал(а):

числять обобщенные силы как сумму работ при обобщённом возможном перемещении — только этот способ нам показывали на парах.

я этот способ не использую и студентам не показываю, так как он легко приводит к ошибкам. если надумаете решать по тем формулам, что я привел выше, то надо нарисовать (и выложить сюда) более подробную картинку: нужно ввести декартову систему координат с центром в точке $O$, ось $y$ направлена вертикально вниз, ось $x$ горизонтальна и направлена вправо, ось $z$ перпендикулярна плоскости рисунка и смотрит от нас. Еще надо пометить буквами все ключевые точки: лифты, точки в которых тросы отходят от шкива и точки в которых крепятся пружины.

[Kink]

Всё-таки попробую вашим способом.
Прошу простить моё незнание редакторов для подобных рисунков и мои кривые линии на реальной бумаге, вот рисунок:


Итак, начнём заново (ну или почти заново). Вывод квадратов скоростей сделал через нашу новую систему координат, но результат тот же.

$$T = \frac{1}{2}(m_1\dot x_1^2+m_2\dot x_2^2+I\dot \varphi^2)$$

Оставлю прежние обозначения: $\overline P_1$, $\overline P_2$ — силы тяжести, $\overline F_1$, $\overline F_2$ — силы упругости пружин, $\overline G_1$, $\overline G_2$ — силы сопротивления демпферов.

$$V = P_1+P_2+F_1+F_2$$

$$P_1 = m_1g, P_2 = m_2g$$

$$F_1 = -c\Delta y_1, F_2 = -c\Delta y_2$$

$$G_1 = \mu \dot y_1, G_2 = \mu \dot y_2$$

где $\Delta y_1$ и $\Delta y_2$ — удлинения/укорочения пружин, а $\dot y_1$ и $\dot y_2$ — скорости грузов относительно троса.
Координата $y$ груза 1 ($x$ и $z$ — постоянны, поэтому для скоростей не важны): $y = OE_1+x_1$, значит абсолютная скорость первого груза $v_1 = \sqrt{\dot x^2+\dot y^2+\dot z^2} = \sqrt{\dot y^2} = \dot x_1$.
Координата $y$ груза 2 ($x$ и $z$ — постоянны, поэтому для скоростей не важны): $y = OE_2-x_2$, значит абсолютная скорость первого груза $v_2 = \sqrt{\dot x^2+\dot y^2+\dot z^2} = \sqrt{\dot y^2} = \dot x_2$.
А теперь сомнительное: $\Delta y_1 = x_1-r\varphi$, $\Delta y_2 = x_2-r\varphi$, $\dot y_1 = \dot x_1-r\dot \varphi$ и $\dot y_2 = \dot x_2-r\dot \varphi$? Относительно скоростей ещё похоже на правду, а вот как находить "дельты" — не могу понять, и тут только предположение.
Далее, как "вгонять" силы в $V$? Если просто так ставить модули сил, то силы тяжести вообще уйдут в никуда.
Если найти $\dot y_1$ и $\dot y_2$, то получится найти то, что справа. Как это сделать, кажется, понятно.

[Oleg Zubelevich]

ну поехали


$\overline M=M \overline e_z,\quad \overline\omega=\dot\varphi \overline e_z$.

Будем считать, что угло $\varphi$ откладывается таким образом, что при $\varphi=0$ со шкива свисают одинаковые хвосты тросса $B_1B_2=D_1D_2=l$.
Через $a$ обозначим игрековою координату правого лифта, через $b$ обозначим игрековою координату левого лифта. Обобщенные координаты в задаче: $a,b,\varphi$. Имеем

$$\overline r_1=a\overline e_y+r\overline e_x,\quad \overline r_2=b\overline e_y-r\overline e_x,\quad \overline r_{D_2}=(l+\varphi r)\overline e_y+r\overline e_x,\quad \overline r_{B_2}=(l-\varphi r)\overline e_y-r\overline e_x$$

Потенциальная энергия:

$$V=-am_1g-bm_2g+\frac{c}{2}(|\overline r_1-\overline r_{D_2}|^2+|\overline r_2-\overline r_{B_2}|^2)=...$$

(считаем, что в раасслабленном состоянии длина пружины равна нулю)

Со стороны демпфера на лифт 1 действует сила $\overline F_1=-\mu(\dot a\overline e_y-\overline v_{D_2})=...$, соответственно на шкив действует сила $\overline F_{D_1}=...$

продолжайте...

[Kink]

$$V=...=-am_1g-bm_2g+\frac{c}{2}(a^2+2l^2+2\varphi^2r^2-2al-2a\varphi r+b^2-2bl+2b\varphi r)$$

$L=T-V$
$\frac{d}{dt}\frac{\partial L}{\partial\dot a}=m_1\ddot a$
$\frac{\partial L}{\partial a}=-m_1g+ca-cl-cr\varphi$

$\frac{\partial \overline v_1}{\partial \dot a}=1$
$\frac{\partial \overline v_2}{\partial \dot a}=0$
$r_3 = 0$
$\frac{\partial \overline v_3}{\partial \dot a}=0$
$Q_1=-\mu(\dot a-r\dot \varphi)$
Первое уравнение системы:

$$m_1\ddot a+\mu(\dot a-r\dot \varphi)+c(r\varphi+l-a)+m_1g=0$$

В ответе в задачнике в качестве обобщенных координат используются $x_1, x_2, \varphi$.
Чтобы свериться, выражаю $x_1$ через $a$, обозначив $l_1=OE_1-l$:
$a=x_1+l+l_1$
$x_1=a-l-l_1$
$\dot x_1=\dot a$
$\ddot x_1=\ddot a$
Получается:

$$m_1\ddot x_1+\mu(\dot x_1-r\dot \varphi)+c(r\varphi -x_1-l_1)=-m_1g$$

Ответ в задачнике:

$$m_1\ddot x_1+\mu(\dot x_1-r\dot \varphi)+c(x_1-r\varphi)=m_1g$$

Если бы не было l_1, то получалось бы, что $V$ нужно умножить на $-1$, чтобы получить такой ответ, или вы сразу выписывали $V$ с отрицательными знаками, подразумевая $L=T+V$?
И как вообще получается $V$?

Тогда пока что ладно, пойдём дальше:
$\frac{d}{dt}\frac{\partial L}{\partial\dot a}=m_2\ddot b$
$\frac{\partial L}{\partial a}=-m_2g+cb-cl+cr\varphi$

$\frac{\partial \overline v_1}{\partial \dot b}=0$
$\frac{\partial \overline v_2}{\partial \dot b}=1$
$\frac{\partial \overline v_3}{\partial \dot b}=0$
$Q_2=-\mu(\dot b+r\dot \varphi)$
Второе уравнение системы:

$$m_2\ddot b+\mu(\dot b+r\dot \varphi)+c(l-b-r\varphi)=-m_2g$$

Проделаем то же самое для сверки ответа, обозначив $E_1E_2=l_2$:
$b = l + l_2 - x_2$
$x_2 = l + l_2 - b$
$\dot x_2 = -\dot b$
$\ddot x_2 = -\ddot b$
Получается:

$$-m_2\ddot x_2+\mu(-\dot x_2+r\dot \varphi)+c(x_2-l_2-r\varphi)=-m_2g$$

$$m_2\ddot x_2+\mu(\dot x_2-r\dot \varphi)+c(r\varphi-x_2+l_2)=m_2g$$

Ответ в задачнике:

$$m_2\ddot x_2+\mu(\dot x_2-r\dot \varphi)+c(x_2-r\varphi)=-m_2g$$

Опять та же проблема...

Oleg Zubelevich в сообщении #1013080 писал(а):

Со стороны демпфера на лифт 1 действует сила $\overline F_1=-\mu(\dot a\overline e_y-\overline v_{D_2})=...$, соответственно на шкив действует сила $\overline F_{D_1}=...$

$\overline F_{D_1}=\mu(\dot a\overline e_y-\overline v_{D_2})=\mu (\dot a-r\dot \varphi)\overline e_y$
$F_{D_1}=\mu (\dot a-r\dot \varphi)$
$\overline F_{B_1}=\mu(\dot b\overline e_y-\overline v_{B_2})=\mu (\dot b +r\dot \varphi)\overline e_y$
$F_{B_1}=\mu (\dot b +r\dot \varphi)$

$\frac{d}{dt}\frac{\partial L}{\partial\dot \varphi}=I\ddot \varphi$
$\frac{\partial L}{\partial \varphi}=2cr^2\varphi-cra+crb$

$\frac{\partial \overline v_{D_2}}{\partial \dot b}=-r$
$\frac{\partial \overline v_{B_2}}{\partial \dot b}=r$
$\frac{\partial \overline v_3}{\partial \dot b}=0$
$Q_3=-r\mu(\dot a-r\dot \varphi)+r(\dot b+r\dot \varphi)=2\mu r^2\dot \varphi+r\mu (\dot b - \dot a)+M$
Третье уравнение системы:

$$I\ddot \varphi-2cr^2\varphi-cr(b-a)-2\mu r^2\dot \varphi-r\mu (\dot b - \dot a)=M$$

Через $x_1, x_2$:
$b-a=l + l_2 -x_2-x_1-l-l_1=-x_1-x_2+l_2-l_1$
$\dot b - \dot a=-\dot x_2-\dot x_1$

$$I\ddot \varphi-2cr^2\varphi+cr(x_1+x_2-l_2+l_1)-2\mu r^2\dot \varphi+r\mu (\dot x_1+ \dot x_2)=M$$

Ответ в задачнике:

$$I\ddot \varphi+2cr^2\varphi-cr(x_1+x_2)+2\mu r^2\dot \varphi-r\mu (\dot x_1+ \dot x_2)=M$$

[Oleg Zubelevich]

Kink в сообщении #1013147 писал(а):

Первое уравнение системы:

$$m_1\ddot a+\mu(\dot a-r\dot \varphi)+c(r\varphi+l-a)+m_1g=0$$

это уравнение у меня получилось таким

$$m_1\ddot a+c(a-l-\varphi r)-m_1g=-\mu(\dot a-\dot\varphi r)$$

($L=T-V$ !!!)
($T=(m_1\dot a^2+m_2\dot b^2+I\dot\varphi^2)/2$)

Наши $a,b$ связаны с $x_1,x_2$ по формулам $a=x_1+y_1,\quad b=y_2-x_2$, где $y_1,y_2$ -- константы (координаты на оси $y$ точек отсчета для переменных $x_1$ и $x_2$ соответственно. Если сравнивать с ответом, то должно быть $y_1=l$. Это равенство должно как-то следовать из условия задачи, из картинки, например.

-- Вс май 10, 2015 15:20:48 --

Kink в сообщении #1013147 писал(а):

Если бы не было l_1, то получалось бы, что $V$ нужно умножить на $-1$, чтобы получить такой ответ, или

проврались вы где-то со знаком

[Kink]

Oleg Zubelevich в сообщении #1013164 писал(а):

проврались вы где-то со знаком

Да, всё-таки нашёл свои минусы (в обоих смыслах ).
Таким образом, с первыми двумя уравнениями разобрался.

Теперь третье уравнение. После поправок со знаками:
$\frac{d}{dt}\frac{\partial L}{\partial\dot \varphi}-\frac{\partial L}{\partial \varphi}=I\ddot \varphi+2cr^2\varphi-cr(a-b)$
$Q_3$ считаем по этой формуле: $Q_j=\sum_{i=1}^N\Big (\overline F_i,\frac{\partial \overline v_i}{\partial \dot q_j}\Big)+\Big(\overline T,\frac{\partial \overline v_A}{\partial \dot q_j}\Big)+\Big(\overline M_A,\frac{\partial \overline \omega}{\partial \dot q_j}\Big)$
Второе слагаемое равно нулю (скорость точки $O$ равна нулю), а третье — $M$.
А вот что с первым. $F_i$ — силы, приложенные к каждому телу нашей системы. Наша система состоит из трёх тел — шкива, грузов 1 и 2? А пружины, демпферы и трос? Что насчёт них? Если бы в нашей системе были ещё точки/тела, скорости которых зависят от $\dot a$ или $\dot b$, то первые два уравнения изменились бы, но их точно нет.

[Oleg Zubelevich]

уравнение на $\varphi$ у меня тоже сошлось с ответом.

Kink в сообщении #1013247 писал(а):

аками:
$\frac{d}{dt}\frac{\partial L}{\partial\dot \varphi}-\frac{\partial L}{\partial \varphi}=I\ddot \varphi+2cr^2\varphi-cr(a-b)$

это верно. непотенциальные активные силы у нас производятся только демпферами и еще момент $M$ имеется. Вот и смотрите , с ккакимми силами демпферы действуют на каждый лифт и на шкив, в каких точках эти силы действуют, с какими скоростями эти точки движутся. Прямо табличку себе составьте прежде чем формулы писать

-- Вс май 10, 2015 18:43:06 --

Kink в сообщении #1013247 писал(а):

А пружины

пружины учтены в потенциальной энергии

-- Вс май 10, 2015 18:50:26 --

Kink в сообщении #1013247 писал(а):

Наша система состоит из трёх тел — шкива, грузов 1 и 2?

да,

Kink в сообщении #1013247 писал(а):

А пружины, демпферы и трос? Что насчёт них?

они невесомы но создают силовое взаимодействие между весомыми телами

[Kink]

Oleg Zubelevich в сообщении #1013255 писал(а):

с ккакимми силами демпферы действуют на каждый лифт и на шкив, в каких точках эти силы действуют

А как определить, к какой точке приложена сила? Нашёл только информацию про силу тяжести (к центру инерции) и силу трения (в точке соприкосновения). И почему вообще демпфер как-то действует на шкив? От вращения шкива трос только перемещается, а демпфер сглаживает/уменьшает растяжение пружины, вызванное силой тяжести груза.

[Oleg Zubelevich]

ну представьте даже, что пружин в системе нет, а есть только демпферы. берете лифт рукой и тяните его вниз, демпфер сопротивляется и тянет трос, тот что выше демпфера, а тросс тянет шкив