Добрый день.
Надеюсь Вы сможете потратить немного своего времени на человека, который рвется к прекрасному (математике), но в его окружении (менеджеров) это крайне непопулярно. Я пишу здесь, потому что мне не с кем обсудить математические проблемы - среди моих знакомых просто нет специалистов в этой области.
Предисловие. В бытность студентом, да и в школьные годы, я старался всегда задавать вопрос "а что если?". Определитель? А что если вычислить его для "кубической матрицы", если я не ошибаюсь, для тензора. И еще миллион таких "а что если?", которые не всегда помогают жить. лучше ведь быть как все, сказали тебе про определитель? Вот заучил определение и сиди.
Прошу не судить строго. Я знаю что я ничего не знаю. И я очень постараюсь употреблять только общепринятые термины. Одно из этих "а что если?" привело меня к вопросу о координатах точки в двухмерном пространстве. Для однозначного определения положения точки в прямоугольной системе координат нужны значения абсциссы и ординаты. А что если мы вспомним о полярной системе координат и введем некоторые допущения?
Представим себе систему координат которая имеет в своей основе спираль Архимеда.
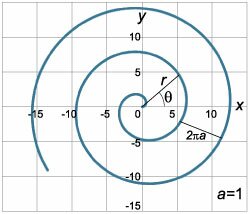
Введем допущение о том, что мы можем однозначно определить положение любой точки лежащей на спирали с помощью лишь одной координаты: числа, которое покажет удаленность точки от начала спирали, точки 0. То есть двигаясь по спирали от точки ноль, мы непременно придем к нашей точке, на каком бы участке спирали она не лежала.
Теперь самая странная часть: введем допущение, что расстояние радиус-вектор r, расстояние между витками спирали, есть точка. Можем назвать это точкой или "неделимой частью данного пространства". С этого момента и начнется критика в мой адрес, но я на самом деле не знаю, как описать это в общепринятых терминах, искренне прошу прощения. Надеюсь, что вы дочитаете до конца. После такого, казалось бы, нелогичного допущения следует логичный вывод: мы можем пронумеровать все точки данной плоскости и однозначно определить положение точки на плоскости одной координатой. Фактически номером точки. не спешите смеяться, дальше будет лучше.
Через точку 0, начало спирали, перпендикулярно плоскости спирали Архимеда проведем линию, которая послужит нам координатной осью, назовем ее прямая А. Теперь мы имеем дело с пространством, в котором положение точки можно однозначно определить двумя координатами: координатой относящейся к положению точки относительно спирали и координатой относящейся к положению точки относительно нашей прямой.
Следующим логичным этапом следует замена прямой А второй спиралью Архимеда, плоскость которой будет так же перпендикулярна первой спирали Архимеда. В этой системе координат мы можем однозначно задать положение точки в четырехмерном пространстве с помощью двух координат. В общем случае с помощью спиралевидных осей координат мы можем задавать точку в n-мерном пространстве n/2 координатами, где n - четное.
Краеугольным камнем является допущение о длине радиус-вектора между спиралями и вообще допущения мысли о таком пространстве, где данное допущение выполнимо. Ведь следую такой же логике мы можем провести такой же мысленный эксперимент в трехмерном и вообще n-мерном пространстве, выбрав точку отсчета и способ определения положения точки в этом пространстве с помощью одной координаты.
Вопрос: имеет ли все вышеперечисленные мысли хоть какое-то отношение к реальным научным трудам, теориям, идеям?Спасибо, что сумели дочитать до конца. Буду очень рад вашим комментариям, даже понимая, что не заслуживаю и на них :)