Эксперименты в области гравитации гораздо сложней ставить, чем наблюдать природные явления. Так что эта область физики вообще преимущественно наблюдательная, а не экспериментальная.
Технические трудности понимаю.
Воспользуюсь случаем спросить - вот правильно ли я понимаю различия в показаниях приборов если бы измерительной точности хватило такой эксперимент поставить -

Не показан третий возможный вариант, когда скорость гравитационных волн равна

, а вот скорость "распространения" статической "силы притяжения" в каком-то смысле мгновенна.
Можно считать, что такой "эксперимент" уже был "поставлен" -- на планетах Солнечной системы.
Стоял следующий вопрос. Вот мы знаем, что в Ньютоновском приближении планеты Солнечной системы притягиваются друг к другу и к Солнцу согласно гравитационному потенциалу Ньютона:

Ещё мы знаем, что уравнение (1) получается в нерелятивистском пределе из ОТО. Ещё мы знаем, что в ОТО поперечно-поперечные гравитационные волны распространяются со скоростью света. Отсюда возникает наивное предположение, а что если и Ньютоновский потенциал

можно бы "улучшить" если предположить, что и он тоже распространяется со скоростью света, а значит, если учесть его запаздывание (а для планет Солнечной системы это ж часы), то мы, якобы, сможем более точно предсказывать траектории планет! Оказалось это совершенно не так. Оказалось, что учёт запаздывания Ньютоновского гравитационного потенциала не улучшает точность расчёта траекторий планет Солнечной системы, а сильно ухудшает (см. работы Тома Фландерна).
Если задуматься над тем почему так происходит, то в голову приходит следующее объяснение. Ньютоновский потенциал получается главным образом из "временных" компонент метрики

,

,

,

, а за поперечно-поперечные гравитационные волны несут ответственность "пространственные" компоненты метрики
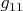
,

,

,

,

,

. Так вот в уравнения ОТО для "пространственных" компонент метрики вторые производные по времени входят, а уравнения для "временных" компонент метрики содержат производную по времени лишь первого порядка, а производной по времени от компоненты

в уравнениях ОТО вообще нет. Поэтому, с одной стороны совершенно не удивительно, что Ньютоновский гравитационный потенциал удовлетворяет уравнению Лапласа, а не Д'Аламбера; а с другой стороны, совершенно не удивительно и то, что поперечно-поперечные гравитационные волны распространяются со скоростью света.