Многочлены 2

[neo66]

Доказать, что, если для функции $f$ из $C^{\infty}[a,b]$: $\forall x \in [a,b]$ $\exists N(x): n\ge N \Rightarrow$ $f^{(n)}(x)=0$, то $f$ - многочлен.

[abc]

юзай теорему бэра)))хотя так вроде получится д-ть что f-мн-н на отрезке вложенном в этот отрезок а дальше как хз

[Скорцонер]

Пусть выполнено условие $f^{(n)}(a) =0, n>N$. Покажем, что тогда $ g(x)=f^{(N+1)}(x) \equiv 0$ на интервале $ [a,b] $. Если считать, что из условия задачи следует ограниченность всех её производных на интервале, $g^{(n)}(x)<M$, то величину $g(x)$ можно оценить по формуле Тейлора. Ясно, что все первые $n$ слагаемых ряда будут равны нулю, поэтому $g(x)$ совпадает с остаточным членом $r$ формулы Тэйлора. Для остаточного члена $r$ имеет место неравенство $r< (b-a)^{n+1}M/(n+1)! $, т.е. $r$ стремится к нулю.

К сожалению, остается главная трудность - доказать ограниченность всех производных.
Может быть что-то получится если действовать через интеграл Фурье, но пока что приходится присоединиться к предыдущему оратору:

abc писал(а):

а дальше как хз

[Скорцонер]

Мне кажется, что теорема неверна.
Построим функцию $f \in C^\infty$ удовлетворяющую условиям задачи, но не являющуюся многочленом.
Сначала отметим известный факт, что существует функция $e (x)= \exp (- \frac {1}{x^2})$ , которая является плоской в нуле, т.е. все её производные равны нулю. С её помощью нетрудно построить для всякого многочлена $P(x) $ гладкую функцию $P(x+e (x)) $, которая будет иметь в нуле те же производные, что и $P(x) $. Если постараться, можно сконструировать функцию $e(x)=e(P(a),Q(b),x) \in C^\infty$, которая в точке $a$ принимает те же значения, что и многочлен $P(x) $ со всеми его производными, а в точке $b$ – те же, что и $Q(x) $.
Построим последовательность функций $f_n(x) $, и покажем, что она сходится к некоторой функции, обладающей требуемыми свойствами.
Сначала строим на отрезке $ [0,1] $ некоторую исходную бесконечно гладкую функцию $f_0(x) $ типа $e(x) $ обращающуюся на концах интервала в нуль со всеми производными.
Затем строим функцию $f_1(x) $. Для этого на средней трети отрезка заменим исходную функцию $f_0(x) $ многочленом $P_1(x) $, (проще всего линейной функцией), с учетом соблюдения непрерывности, оставляя пока на $ [0,1/3] $ и $ [2/3,1] $ величину $f_0(x) $ неизменной.
После этого на отрезке $ [1/3-\epsilon, 1/3] $ c некоторым подходящим $ \epsilon>0$ заменим исходную функцию $ f_0(x) $ также на функцию типа $ e(x) $, но потребуем, чтобы значения её и всех её производных на концах интервала слева – совпадали с функцией $f_0(x) $ , а справа – совпадали с их значениями для локального многочлена $P_1(x) $.
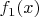
На правом интервале $ [2/3, 2/3+\epsilon] $ достроим $f_1(x)$, также потребовав равенства всех производных справа и слева.

Строим далее функцию $f_2 (x) $. Для этого на каждом из двух интервалов $ [0,1/3] $ и $ [2/3,1] $, где $f_1(x) $ не есть многочлен, вырезаем среднюю часть и снова заменяем на них функцию $f_1(x) $ локальными многочленами. Соединим многочлены и участки гладких функций новыми кусками гладких функций на участках (длины $\epsilon) : [1/9 - \epsilon, 1/9], [2/9, 2/9+\epsilon], [7/9-\epsilon, 7/9], [8/9, 8/9+\epsilon] $, выбирая их с условием совпадения всех производных на концах интервалов. При этом, как легко видеть, росток (germ) функции в однажды построенных точках сопряжения мы не трогаем.

Процесс построения функций $f_n (x) $ может быть неограниченно продолжен.
Нетрудно видеть, что, при $n \to \infty$ будет существовать предельная функция $f_n (x) \to f_{\infty }(x) $ . Любая точка из области определения $f_ {\infty }(x) $ будет либо принадлежать окрестности, в которой функция локально равна некоторому многочлену, образованному при построении некоторой $f_n (x) $, и больше не меняющемуся с увеличением $n$ , либо будет концевой точкой области определения этого (локального) многочлена. Поскольку на каждом этапе построения (для каждого $n$) в концевых точках функция $f_n (x) $ будет обладать всеми производными, совпадающими с производными многочлена, то же будет справедливо и для предельной функции.
Требуемая функция получена.

[Юстас]

Честно говоря, не хочется искать ошибку в Вашей словесно описанной конструкции, могу только сказать, что утверждение задачи верно и очень известно. Решение, которое я видел, использует теорему Бэра.

[worm2]

Скорцонер писал(а):

Поскольку на каждом этапе построения (для каждого $n$) в концевых точках функция $f_n (x) $ будет обладать всеми производными, совпадающими с производными многочлена, то же будет справедливо и для предельной функции.

Утверждение вызывает сомнение. Не ясно, как можно довести до строгого доказательства даже того, что предельная точка будет в этой точке дифференцируема. Сравните:
Функцию y=|x| можно бесконечно приближать последовательностью бесконечно дифференцируемых функций, у каждой из которых в нуле производная будет равна 0. Но предельная функция не имеет производной в нуле вообще.

[maxal]

В первом выпуске (1997) Мат.Прос. в качестве задачи 10 сформулировано более сильное утверждение:

Доказать, что для функции $f \in C^{\infty}(\mathbb{R})$, если $\forall x\in \mathbb{R}\ \exists n : f^{(n)}(x)=0$, то $f$ - многочлен.

Решение этой задачи приведено в выпуске 4 (2000).

[Скорцонер]

Я заглянул в теорему Бэра, и даже нашел в И-нете решение подобной же задачи для класса аналитических функций. Действительно, из т. Бэра вытекает, что множество $C_n$, на котором n-я производная функции равна нулю, при некотором $n$ имеет внутри себя всюду плотный интервал. (Если бы такого $n$ не существовало, то объединение $C_n $было бы тоже нигде не плотным). Т.е. на этом интервале функция является многочленом. Аналитически продолжая, найдем, что она везде тоже есть многочлен.
Приблизительно в этом направлении я пытался продвинуться, и уже писал здесь о том, что мера множества, на котором $f^{(n)} $отлична от нуля $\to 0$. (Потом, правда, за ненадобностью это убрал). Ясно, что от аналитических функций до $C^{\infty}$ дистанция, так сказать, огромного размера.
Затем я посмотрел решение задачи в Мат. Просвещении за 2000 г., на которое сослался Maxal. Мне сильно показалось, что автор Д.Бураго снова доказывает все только для аналитических функций. Он почему-то полагает, что функция из $ C^{\infty}$ определяется своим рядом Тэйлора и не предусматривает возможности гладкой «сшивки» функций из $C^{\infty}$ в отдельных точках.

Согласен, что приведенное выше рассуждение тоже трудно считать строгим доказательством. Но пока можно надеяться, что оно может быть улучшено.

Будет ли построенная функция дифференцируема в точках сопряжения? Сильно упрощая ситуацию, сведем вопрос к поведению предельной функции в одной лишь точке сопряжения, например, в нуле. По тому же принципу замещения полиномами, что и выше, построим следующую функцию:
Снова будем исходить из функции $e (x)= \exp (- \frac {1}{x^2})$, и заменим её на всех участках вида $[\frac{1}{2k},\frac {1}{2k+1}] $ линейной функцией по непрерывности. Ясно, что полученная функция будет дифференцируемой в нуле. Также можно написать выражение для $ n$-й производной в нуле через конечные разности. Устремляя их к нулю, найдем, что и $f^{(n)}(0) = 0$.

В общем, для более строгого обоснования построенного примера желательно для начала доказать такой правдоподобный факт:
1). Пусть $x \in[0, 1], f(x) \in C^\infty$. Задана монотонно сходящаяся к нулю последовательность точек $x_n$. Исходя из $f(x) $ строится функция $f^* (x) \in C^\infty$ по следующему правилу. На некоторых отрезках $ [x_k, x_{k+1}]$ функция $ f^* (x) = f(x) $ (остается неизменной), на некоторых $ f^* (x) $ равна линейной аппроксимации $ f(x) $. В этом случае на отрезках справа и слева от линейного участка функция $f^* (x) $ определяется таким образом, чтобы имело место гладкое (по всем производным) сопряжение с соседними участками.
Надо показать, что способ сопряжения всегда можно выбрать так, что в нуле все производные $f^* (x) $ и $f(x) $ совпадают.

Подозреваю, что ошибки вполне могут где-то крыться, но нужны или более конкретные возражения, или явное доказательство высказанной neo-66 теоремы.

.

[worm2]

Для аналитических функций это слишком простая задача. Множество нулей аналитической функции, не равной тождественно нулю, не более чем счётно. Т.к. любая производная аналитической функции также является аналитической, то, объединяя множество нулей функции и всех её производных, получаем либо (1) какую-то производную, тождественно равную нулю, либо (2) не более чем счётное множество. А т.к. по условию задачи это множество есть отрезок [a,b], т.е. несчётное множество, то реализуем только случай (1). И никакого Бэра не надо.

[maxal]

Вот решение из Мат.Прос. N4:

Цитата:

Решение 1.10 (Д. Ю. Бураго)
Функция, заданная на всей вещественной прямой, бесконечно дифференцируема. В каждой точке некоторая производная (номер производной может зависеть от точки) равна нулю. Докажите, что эта функция - многочлен.

Обозначим рассматриваемую функцию через $f$. Для каждого многочлена $p$ построим замкнутые множества

$$M'_p=\{x\mid f(x)=p(x)\},$$

$$M_p=M'_p\setminus\{x\mid x\ \text{изолированная точка }M'_p\}$$

и докажем, что для какого-то $p$ выполнено $M_p=\mathbb{R}$.

Покажем, что $M_{p_1}\cap M_{p_2}=\emptyset$ при $p_1\ne p_2$. Каждая точка множества $M_p$ по построению является предельной, а ряд Тейлора $f$ в предельной точке $x_0\in M_p$ однозначно восстанавливается по значениям функции на $M_p\setminus\{x_0\}$. Действительно, предположим обратное. Пусть для некоторых двух функций $f_1,f_2\in C^\infty$ с несовпадающими в $x_0$ рядами Тейлора при $x_n\to x_0$ ($x_k\ne x_0$, $k>0$) выполнено $f_1(x_n)=f_2(x_n)$. Тогда функция $g=f_1-f_2$ обращается в 0 на $\{x_n\}$ (сколь угодно близко от $x_0$), а ее ряд Тейлора - ненулевой. Применяя формулу Тейлора для первого ненулевого члена ряда Тейлора функции $g$, приходим к противоречию.

Обозначим $N=\mathbb{R}\setminus\cup_p M_p$. Это открытое множество. Докажем, что $N$ пусто, после чего из связности $\mathbb{R}$ заключим, что ровно одно $M_p$ непусто (что и требуется доказать).

Итак, предположим, что $N$ непусто. Обозначим через $F^{(n)}$ множество нулей $n$-й производной $f$. Построим систему вложенных интервалов $\Delta_i$ индуктивно. Выберем произвольно интервал $\Delta_0\subset N$, а каждый интервал $\Delta_{n+1}$ выберем в открытом непустом множестве $\Delta_n\setminus F^{(n+1)}$ (если $\Delta_n\subset F^{(n+1)}$, то $f$ совпадает с многочленом на $\Delta_n$). Нетрудно видеть, что в точках $\cap_{n=0}^\infty \Delta_n$ все производные $f$ отличны от 0. Пришли к противоречию.

[Скорцонер]

Да, Бураго прав, и мои критики тоже. Должен сознаться, что я был недостаточно внимателен, просматривая его решение. Проще всего опровергнуть мой «контрпример» ссылкой на т. Бореля, о том, что отрезок [0,1] нельзя покрыть никакой системой непересекающихся интервалов c общей мерой =1 (на которых определены локальные полиномы), на что я, собственно, надеялся. Ну что ж, надо действительно «учить матчасть» к чему постоянно склоняет нас один из завсегдатаев форума.

[lofar]

Д. Ю. Бураго писал(а):

Каждая точка $M_p$ по пострению является предельной.

Если из замкнутого множества выбросить все изолированные точки, то в остатке могут появиться новые изолированные точки. Для примера можно взять $M=\{0\}\cup\{1/n|n\in\mathbb N\}$.

[Someone]

lofar писал(а):

Д. Ю. Бураго писал(а):

Каждая точка $M_p$ по пострению является предельной.

Если из замкнутого множества выбросить все изолированные точки, то в остатке могут появиться новые изолированные точки. Для примера можно взять $M=\{0\}\cup\{1/n|n\in\mathbb N\}$.

Видимо, следовало написать

$$M_p=\{x\in M_p':\text{для каждой окрестности }Ux\subseteq\mathbb R\text{ множество }Ux\cap M_p'\text{ несчётно}\}$$

.
Тогда множество $M_p'\setminus M_p$ счётно и нигде не плотно в $\mathbb R$, а $M_p$ заведомо не имеет изолированных точек.

[тоша]

Цитата:

Обозначим $N=\mathbb{R}\setminus\cup_p M_p$. Это открытое множество.

Не знаете, почему оно открытое?..

[Taras]

$M_p$ - замкнутое.