Ранг матрицы из квадратов

[xolodec]

Пусть есть матрица размера n на n

$$\begin{pmatrix} 0 & 1 & 4 & \cdots & (n-1)^2 \\ 1 & 0 & 1 & \cdots & (n-2)^2 \\ 4 & 1 & 0 & \cdots & \vdots \\ \cdots & \cdots & \cdots & \ddots & \vdots\\ (n-1)^2 & (n-2)^2 & \cdots & \cdots & 0 \end{pmatrix}$$

Данная матрица симметрическая, то есть она подобна некоторой диагональной.
Что бы найти ранг исходной матрицы достаточно найти кратность собственного значения $\lambda = 0$.
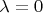
Но как найти эту кратность - хороший вопрос и я не знаю пока на него ответ. Мне кажется, что эта кратность равна нулю, но как это показать строго - не наю.
Вторая моя идея - это доказать, что не существует одновременного решения слау

$$\left\{ \begin{array}{rcl} 0x_1 + 1x_2 + \cdots + (n-2)^2 x_{n-1} &=& (n-1)^2 \\ \hdotsfor{3} \\ (n-1)^2 x_1 + (n-2)^2 x_2 + \cdots + x_{n-1} &=& 0 \end{array} \right.$$

Как это сделать, однако, также для меня пока вопрос.
Можете подсказать, пожалуйста, куда двигаться ?

[VladimirKr]

Можно попробовать представить данную матрицу как многочлен от циркулянтной матрицы (сопровождающая матрица многочлена $\lambda^n-1$) и просто выписать собственные числа.

[GDTD]

Пусть $n\ge 4$. Вычтете из первой строки вторую, из второй третью, ..., из предпоследней последнюю. В полученной матрице вычтете из первой строки вторую, ..., из предпредпоследней предпоследнюю. Далее вроде очевидно.

[patzer2097]

xolodec, Ваша матрица равна $A+B+C$, где $a_{ij}=i^2$, $b_{ij}=j^2$, $c_{ij}=-2ij$; матрицы $A,B,C$ имеют ранг $1$. Это самое простое решение, как мне кажется

[svv]

(patzer2097)

patzer2097 в сообщении #1007582 писал(а):

Это самое простое решение, как мне кажется

Вы согласны, что бывает так, что решение B некоторой задачи короче и его проще понять, чем решение A, но для его отыскания нужно проделать некоторую дополнительную работу, за которую автор решения обычно великодушно не требует счёт, как будто оно свалилось с неба или лежало прямо на дороге?

Элементы $a_{ik}$ любой строки — значения некоторого полинома второй степени от $k$. Значит, линейная комбинация (третья разностная производная) $1a_{i,k-3}-3a_{i,k-2}+3a_{i,k-1}-1a_{i,k}=0$. Значит, каждый столбец с $k>3$ является линейной комбинацией трех предыдущих. Следовательно, каждый столбец является линейной комбинацией первых трех.

xolodec в сообщении #1007523 писал(а):

Вторая моя идея - это доказать, что не существует одновременного решения слау

$$\left\{ \begin{array}{rcl} 0x_1 + 1x_2 + \cdots + (n-2)^2 x_{n-1} &=& (n-1)^2 \\ \hdotsfor{3} \\ (n-1)^2 x_1 + (n-2)^2 x_2 + \cdots + x_{n-1} &=& 0 \end{array} \right.$$

Как это сделать, однако, также для меня пока вопрос.

Это же рассуждение говорит о том, что $(0,0,0,...,0,0,1,-3,3)$ — решение.

[patzer2097]

(svv)

svv в сообщении #1007584 писал(а):

Вы согласны, что бывает так, что решение B некоторой задачи короче и его проще понять, чем решение A, но для его отыскания нужно проделать некоторую дополнительную работу, за которую автор решения обычно великодушно не требует счёт, как будто оно свалилось с неба или лежало прямо на дороге?

Да. Но не понимаю, как Ваше замечание относится (и относится ли) к моему решению и этой задаче.

[svv]

(Оффтоп)

Не относится, я просто хотел пофилософствовать: простота разная бывает. Например: три часа искал уникально короткое решение и нашел-таки. А чуть более сложное было очевидным.

[ewert]

(Оффтоп)

На самом деле оптимально решение GDTD. Оно ничуть не длиннее других и, что главное, напрашивается. Решение svv -- в сущности, то же самое, но требует знания дополнительной теории, причём не относящейся к линейной алгебре и которой студенты к этому моменту заведомо не владеют. Решение patzer2097 элегантно, однако тоже на этот момент недоступно, да и неполно: ну не превосходит трёх; ну и что?...

[patzer2097]

(svv)

svv в сообщении #1007606 писал(а):

Не относится, я просто хотел пофилософствовать

OK, я тоже понял, что Вы не о математике

(ewert)

ewert в сообщении #1007610 писал(а):

Решение patzer2097 элегантно, однако тоже на этот момент недоступно

недоступно - не читайте

ewert в сообщении #1007610 писал(а):

да и неполно

а "полные" в Вашем смысле я писать и не привык; более того, на этом форуме "полные", как мне кажется, писать и не принято

[ewert]

(Оффтоп)

patzer2097 в сообщении #1007613 писал(а):

недоступно - не читайте

Я-то, как видите, прочитал. А вот ТС, как видите -- нет. Попытайтесь-ка сформулировать теоремку о сумме одноранговых матриц, на которую Вы намекали, а потом посмотрите, в каком месте учебника она находится. Если вообще находится, что далеко не факт. Задачка же между тем вполне шаблонна.

[svv]

(Оффтоп)

ewert в сообщении #1007610 писал(а):

На самом деле оптимально решение GDTD. Оно ничуть не длиннее других и, что главное, напрашивается.

Оно действительно напрашивается, но почему оно это делает? А потому что мы откуда-то знаем, что если взять разности соседних значений полинома $n$-й степени от целочисленной переменной, получится полином $(n-1)$-й степени. Или не знаем? Тогда оно уже не напрашивается и может найтись только методом тыка.

Это дополнение к тому, о чем я писал выше: решение исключительно легко проверяется, но чтобы его неслучайно найти, надо что-то знать.

[ewert]

(Оффтоп)

svv в сообщении #1007618 писал(а):

Оно действительно напрашивается, но почему оно это делает? А потому что мы откуда-то знаем, что если взять разности соседних значений полинома $n$-й степени от целочисленной переменной,

Нет, совсем не поэтому. А просто потому, что это наиболее шаблонный приём: не знаешь, что делать -- попробуй чего-нибудь повычитать, авось чего упростится. Ну и тут на первом же ходу упрощается, даже если ничего не знать ни про многочлены, ни, упаси боже, про конечные разности.

[patzer2097]

(ewert)

ewert в сообщении #1007615 писал(а):

А вот ТС, как видите -- нет.

пока никак не вижу, честно говоря

ewert в сообщении #1007615 писал(а):

Попытайтесь-ка сформулировать теоремку о сумме одноранговых матриц, на которую Вы намекали

не знаю такой теоремки, поэтому оставлю это упражнение для Вас

ewert в сообщении #1007615 писал(а):

а потом посмотрите, в каком месте учебника она находится. Если вообще находится, что далеко не факт.

учебники бывают разные

[ewert]

(Оффтоп)

patzer2097 в сообщении #1007622 писал(а):

не знаю такой теоремки, поэтому оставлю это упражнение для Вас

Тогда у Вас нет решения. Тогда всё, что Вы можете утверждать -- это что не выше трёх.

[patzer2097]

(ewert)

ewert в сообщении #1007624 писал(а):

Тогда у Вас нет решения. Тогда всё, что Вы можете утверждать -- это что не выше трёх.

OK, спасибо, что разрешили утверждать хоть это