Как правильно представлять себе дифференциал?

[Pulseofmalstrem]

Доброе время суток.
Так как основную часть своего внимания я все-таки уделил физике, то у меня на данном этапе сложилось видение дифференциала как маленького кусочка чего-то там (при решение разного рода простеньких задачек вроде нахождения центра масс всегда удобно рассматривать маленькие части тела, а потом интегрировать).
Однако такое видение очевидно ущербно в математическом смысле, когда я пытаюсь представить себе дифференциал боллее строго, то мне в голову лезет треугольничек, в котором горизонтальный катет суть есть приращение аргумента функции, а острый угол - арктангенс производной; тогда дифференциал - вертикальный катет. Впрочем, по всей видимости это тоже ущербно.

[Hasek]

Если вопрос "Как представлять себе дифференциал?", то как некий линейный непрерывный оператор, хорошо приближающий функцию в малой окрестности рассматриваемой точки.

[Pphantom]

Pulseofmalstrem в сообщении #1005850 писал(а):

Однако такое видение очевидно ущербно в математическом смысле, когда я пытаюсь представить себе дифференциал боллее строго, то мне в голову лезет треугольничек, в котором горизонтальный катет суть есть приращение аргумента функции, а острый угол - арктангенс производной; тогда дифференциал - вертикальный катет. Впрочем, по всей видимости это тоже ущербно.

Почему же? Дифференциал - линейная часть приращения функции, так что это вполне адекватно. Идея про малость дифференциала связана лишь с тем, что для "достаточно хороших" функций при малом приращении аргумента приращение функции близко к ее дифференциалу.

[VanD]

Дифференциал отображения - это его линеаризованное действие.
В то время, как отображение действует на многообразии, его дифференциал орудует в касательном пространстве. Когда в обиход входят нелинейные отображения, представление вектор - направленный отрезок - становится неудобным. Даже под действием отображений $\mathbb{R}^n$ в себя направленные отрезки становятся иногда не отрезками вовсе и линейная структура не сохраняется. Тогда касательное пространство в точке сделали самим по себе - отдельным, абстрактным. И отображения уже не действуют на касательном пространстве непосредственно. Поэтому рассматривают действие линеаризованного отображения на касательном пространстве - его дифференциала. При этом дифференциалы действуют очень удобно - они вектор скорости кривой в точке прообраза переводят в скорость к кривой-образу в точке-образе.

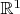
Дифференциал функции - частный случай описанного выше. Будучи оператором из некоторого линейного пространства $V$ в $\mathbb{R}^1$, он являет собой ковектор на $V$.

[Munin]

Я вам вот что скажу. Математики вам расскажут подробности про оператор и всякое такое.

Но это не будет ответом на вопрос "как правильно представлять себе дифференциал?". Потому что "представлять себе" - это не строгое занятие, не того же уровня, что "доказать теорему". Это - то, что вы держите в голове для рассуждений.

И ответов на вопрос "как правильно представлять себе дифференциал?" - множество разных! Как удобней! Так, чтобы хорошо получалось рассуждать. А рассуждаете вы на разные темы: иногда на физические, иногда на математические. Рассуждаете над разными задачами, разного типа и разной сложности. И там везде нужны свои представления о дифференциале. Везде оптимальны - разные. Но годятся часто и не самые оптимальные.

Так что, не давайте себе запудрить голову тем, что "такое видение очевидно ущербно в математическом смысле". Лучше запасайтесь разными представлениями! И "маленький кусочек" работает (в одних задачах - в физических), и "треугольничек" (в других задачах - в математических). И ещё несколько вариантов у вас могут вырасти - и им тоже могут найтись сферы применения.

[AGu]

Прально. Вот мудёр Munin, как ни крути, мудёр.

P.S. Я чаще всего представляю себе такую мааахонькую касательную (прямую или плоскость), а в точке касания — такое малюююсенькое начало координат (перенесенное из бывшего начала).

[Brukvalub]

(Оффтоп)

Чтобы наглядно увидеть дифференциал, достаточно разобрать задний мост автомобиля ГАЗ-53.

[svv]

(Оффтоп)

Brukvalub в сообщении #1006495 писал(а):

Чтобы наглядно увидеть дифференциал, достаточно разобрать задний мост автомобиля ГАЗ-53.

Я понял! А второй дифференциал — это нужно два задних моста.

[Munin]

(Оффтоп)

Касательная - это хорошо для дифференциалов функций. Но есть ещё и дифференциалы независимых переменных. Есть дифуры в форме записи "в дифференциалах". И наконец, ещё есть коварный случай, когда написано $dy,$ но это вообще не дифференциал, а "внешний дифференциал" - штука, аналогичная производной или градиенту.

Brukvalub
:-)

[svv]

Мнение:

Цитата:

Обозначение $df/dx$, всегда представлявшееся преувеличенно соблазнительным, породило многие (обычно бессмысленные) определения для $df$ и $dx$ самих по себе, единственной целью которых было придать смысл равенству

$$df=\frac{df}{dx}\cdot dx\;.$$

Для $f:\textbf R^2\to\textbf R$, например, $df$ определяется в классических курсах формулой

$$df=\frac{\partial f}{\partial x} dx+\frac{\partial f}{\partial y} dy$$

(что бы ни означали $dx$ и $dy$).

М. Спивак. Математический анализ на многообразиях.

[fronnya]

Сивухин, 1 том, гл.1, параграф 1, пункт 5 ( о связи физики с математикой)

[sergei1961]

Да нельзя его просто и строго определить в начальном курсе. Или нестрого, или непросто.

[AGu]

(Оффтоп)

sergei1961 в сообщении #1006738 писал(а):

Да нельзя его просто и строго определить в начальном курсе.

Грустная новость.

[g______d]

Munin в сообщении #1006509 писал(а):

когда написано $dy,$ но это вообще не дифференциал, а "внешний дифференциал" - штука, аналогичная производной или градиенту.

Это одно и то же.

[svv]

Но второй внешний дифференциал равен нулю.