День добрый.
Пусть движение СС задано в форме Эйлера:

,

,

,
где

- координаты точек среды в начальном состоянии,

- в деформированном состоянии.
Тензор деформаций Альманси:
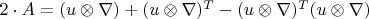
,
где градиент вектора

в цилиндрической с.к. (с учетом

) имеет вид:

Запись

означает частное дифференцирование компоненты вектора.
Тогда компоненты тензора Альманси имеют вид:

,

,

.
Подскажите, пожалуйста, все ли правильно я сделал?