[Линейная алгебра] Прошу проверить решения

[kp9r4d]

Все задачи взяты отсюда, решения в эту тему буду выкладывать по мере.

Во всех задачах пространства полагаются конечномерными, если не оговорено обратное. Основное поле полагается $\mathbb{C}$, если не задана евклидова структура и $\mathbb{R}$ иначе.

Задача 1.1
Постройте два некоммутирующих диагонализируемых оператора.
Решение
Рассмотрим двумерное векторное пространство и рассмотрим два базиса в нём: $(e_1, e_2)$ и $(f_1, f_2)$, связанных соотношениями $e_2 = f_2, e_1 = -2f_1 + 2f_2$. Тогда операторы $L_1, L_2$, задаваемые соотношениями:

$$L_1(e_1) = 2e_1$$

$$L_1(e_2) = e_2$$

$$L_2(f_1) = 2f_1$$

$$L_2(f_2) = f_2$$

Очевидно диагонализируемы (невырожденые операторы из двумерного п-ва в двумерное, которые имеют два линейно независимых собственных вектора) но:

$$L_2(L_1(e_1+e_2)) = L_2(2e_1+e_2) = L_2(-4f_1+4f_2+f_2) = -8f_1+5f_2$$

$$L_1(L_2(e_1+e_2)) = L_1(L_2(-2f_1+3f_2)) = L_1(-4f_1+3f_2) = L_1 (2e_1-e_2) = 4e_1 - e_2$$

$$L_1(L_2(e_1+e_2)) = 4e_1 - e_2 = -8f_1 +7f_2 \neq -8f_1+5f_2 = L_2(L_1(e_1+e_2))$$

Задача 1.2
Оператор диагонализируем, когда его характеристический многочлен не имеет кратных корней.
Решение
Я решил только, если все корни ненулевые. Если у характеристического многочлена столько различных корней, какова и размерность матрицы $A$, то решив уравнение $Ax = \lambda x$ для каждого собственного числа $\lambda$, мы найдём, как минимум, $\operatorname{dim} V$ инвариантных одномерных подпространств. Для тех $\lambda$, для которых размерность пространства решений этого уравнения больше одного, выберем любое одномерное подпространство. Из каждого найденного одномерного подпространства выберем по ненулевому вектору. Получим систему $x_i$ из $\operatorname{dim} V$ собственных векторов, покажем, что она линейно независима. Выберем максимальную независимую подсистему $x_{i_k}$ пусть её размер $< \operatorname{dim} V$. Выберем из системы $x_i$ вектор $x_{u}$ не вошедший в независимую подсистему $x_{i_k}$. Выразим его через независимую подсистему

$$x_{u} = \sum_k c_k x_{i_k}$$

Подействуем на обе части уравнения оператором, каждый $x_i$ увеличиться в собственное число раз.

$$\lambda_{u} x_{u} = \sum_k c_k \lambda_{i_k} x_{i_k}$$

Разложим $x_{u}$ снова в сумму

$$\lambda_{u} \sum_k c_k x_{i_k} = \sum_k c_k \lambda_{i_k} x_{i_k}$$

$$\sum_k c_k (\lambda_{u} - \lambda_{i_k}) x_{i_k} = 0$$

так как система линейно независимая получаем равенства

$$\lambda_{u} = \lambda_{i_0} = \lambda_{i_1} = ...$$

что противоречит тому, что все собственные числа различны.

Задача 1.3
Найти все инвариантные подпространства жордановой клетки
Решение
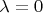
Единственное собственное значение жордановой матрицы: это $\lambda$. Если $\lambda = 0$ то единственное инвариантное подпространство - подпространство размерности 0. В дальнейшем считаем, что $\lambda \neq 0$. Выписав покоординатно систему уравнений $Ax=\lambda x$ где $A$ - жорданова клетка получим следующее:

$$ \begin{cases} x_1 \lambda + x_2 = \lambda x_1 \\ x_2 \lambda + x_3 = \lambda x_2 \\ ... \\ x_{n-1} \lambda + x_n = \lambda x_{n-1} \\ \lambda x_n = \lambda x_n \end{cases} $$

Откуда видно, что единственное инвариантное подпространство, это $(t,0,0,...,0)$ $t \in \mathbb{C}$.

Задача 1.5
Равенство $AB - BA = \operatorname{Id}$ невозможно
Решение
В левой части след равен 0, а в правой нет.

Задача 1.6
Характеристические многочлены $AB$ и $BA$ совпадают

Задача 1.7
Если $AB - \operatorname{Id}$ обратим, то и $BA- \operatorname{Id}$ обратим.
Решение
Следует из предыдущей задачи, если характеристические многочлены совпадают, то и их значения в точке $1$ также совпадают. Значение характеристического многочлена оператора $A$ в точке 1, это как раз $\det (A - E)$. Так как определители левой и правой части нулевые или ненулевые одновременно, то и сами эти части обратимы или необратимы одновременно.

Задача 1.8
Число решений уравнения $x^2 = A$ конечно и равно $2^k$ где $k$ - размерность пространства для почти всех операторов $A$.
Решение
Пусть $\operatorname{dim} V = n$ Множество операторов, у которых есть $n$ различных инвариантных одномерных подпространств, сумма которых равна всему пространству, плотно в пространстве всех операторов. По этим подпространствам однозначно восстанавливается оператор. Теперь построим оператор, который имеет ровно такие же инвариантные подпространства, но если у исходного инвариантные подпространство переводило каждый вектор $v$ в вектор $\lambda v$, то построенный будет переводить $v \mapsto \sqrt{\lambda} v$. У любого числа, кроме нуля, ровно два квадратных корня, то есть, подобный оператор можно построить $2^n$ способами.

Задача 1.9
Если $\operatorname{Tr} A^k = 0$ для почти всех $k$, то $A$ - нильпотент.
Решение
Перейдём к жордановому базису. От смен базиса характеристический многочлен не изменяется. Приведя подобные члены при $\lambda$ в характеристическом многочлене можно увидеть, что коэффициент при $\lambda^{n-1}$ равен $-\operatorname{Tr} A$. По теореме Виета, этот коэффициент равен сумме корней, взятой со знаком минус. Итого: след матрицы равен сумме её собственных чисел. По тем же соображениям, для любого натурального $k$ справедливо:

$$\operatorname{tr} A^k = \sum_i a_i^k$$

отсюда следует, что $x_i = 0; i = 1..n$ (даже если выполнены почти все равенства). Итак, у нашего оператора все собственные значения нулевые. В жордановом базисе у его матрицы на диагонали и под нею будут стоять нули. Такой оператор занулится после, максимум, $\operatorname{dim} V$ умножений.

[patzer2097]

Вроде бы всё правильно, кроме задачи 1.3. По поводу 1.6 - эту задачу достаточно решить для обратимой матрицы $A$. Еще несколько наблюдений:

1.2. На самом деле Вы решили задачу полностью - достаточно заметить, что $A$ диагонализируем тогда и только тогда, когда $A+\lambda E$ диагонализируем.

1.3.

kp9r4d в сообщении #930484 писал(а):

Единственное собственное значение жордановой матрицы: это $\lambda$. Если $\lambda = 0$ то единственное инвариантное подпространство - подпространство размерности 0.

Это неверно, т.к. у жордановой клетки есть собственный вектор..

1.8. Вам нужно было проверить, что почти все операторы имеют $2^k$ квадратных корней, а Вы проверили это только для некоторого плотного множества операторов.

1.9. Было бы еще интересно указать, как именно из равенств $\sum_i a_i^k=0$ следует, что $a_i=0$.

[kp9r4d]

patzer2097 в сообщении #930499 писал(а):

Вам нужно было проверить, что почти все операторы имеют $2^k$ квадратных корней, а Вы проверили это только для некоторого плотного множества операторов.

Я думал это и значит «почти все», а имеется в виду, все, кроме конечного числа?

patzer2097 в сообщении #930499 писал(а):

Было бы еще интересно указать, как именно из равенств $\sum_i a_i^k=0$ следует, что $a_i=0$.

Будем доказывать более общее утверждение, о том, что если для ненулевых $c_i$ и любых $x_i$ и почти всех $k$ верно, что

$$\sum_i c_i x_i^k = 0 $$

то все $x_i = 0$.
Возьмем достаточно большое $m$, с которого эти равенства начинают выполняться. Выбросим все нулевые переменные. Выбросим также все равные: если $x_i = x_j$ то можно выбросить их обеих и вместо них добавить $y = x_i = x_j$ с коэффициентом $c_i +c_j$ (если он равен нулю, то их можно просто выбросить). В дальнейшем все показатели степеней будут полагаться $>m$. Для каждого $k$ проделаем следующее:
$c_1 x_n x_1^k + c_2 x_n x_2^k + ... + c_n x_n^{k+1} = 0$
$c_1 x_1^{k+1} + c_2 x_2^{k+1} + ... + c_n x_n^{k+1} = 0$
Вычитая, получим
$c_1 x_1^k(x_1 - x_n) + c_2 x_2^k(x_2 - x_n) + ... + c_{n-1} x_{n-1}^k(x_{n-1} - x_n) = 0$
повторив конструкцию, получим снова:
$c_1 x_1^k(x_1 - x_n)(x_1 - x_{n-1}) + c_2 x_2^k(x_2 - x_n)(x_2 - x_{n-1}) + ... + c_{n-2}x_{n-2}^k(x_{n-2} - x_{n})(x_{n-2} - x_{n-1}) = 0$
повторив ещё $n-3$ раза получим
$c_1 x_1^k(x_1 - x_n)(x_1 - x_{n-1})...(x_1 - x_2) = 0$
Отсюда получим, что либо $x_1 = 0$, либо $c_1 = 0$ либо какие-то две переменные равны, и того и другого и третьего быть не может по предположению.

Насчёт 1.2 и 1.3 ещё подумаю, спасибо в любом случае.

[patzer2097]

kp9r4d в сообщении #930517 писал(а):

Я думал это и значит «почти все», а имеется в виду, все, кроме конечного числа?

Не знаю, что имеется в виду, но думаю, что что-то типа "везде, кроме множества меры нуль". Дело в том, что если понимать слово "почти" в Вашем смысле, то придется признать, например, что "почти все числа рациональны".

[kp9r4d]

patzer2097
Ну да, но множество операторов, например, у которых хотя бы пара корней характеристического многочлена совпадают или хотя бы один корень ноль имеет меру нуль. А всё остальное, вроде как, подходит.

Как вы думаете, а в задаче 1.10 что понимается под «наложением»? В гугле прочёл, что это изометрия, тогда относительно какой метрики? Порождаемой скалярным произведением: $(p,q) = \int_0^1 p(x)q(x)dx$ ?

В 1.6 для обратимых почти очевидно. Определители у $A^{-1}(AB - \lambda E)$ и $(BA - \lambda E)A^{-1}$ совпадают, а оба этих определителя в точности в $\det(A^{-1})$ больше, чем определители исходных. И всё это для любого $\lambda$.

[patzer2097]

Про 1.10 не знаю, в 1.8 надо пояснить, почему это множество имеет меру нуль, а в 1.6 осталось заметить, что обратимые операторы образуют плотное множество.

[kp9r4d]

patzer2097 в сообщении #930536 писал(а):

в 1.8 надо пояснить, почему это множество имеет меру нуль

Сопоставим каждому оператору какую-нибудь его жорданову матрицу. Каждое из соотношений
$a_{11} = a_{22}$
$a_{11} = a_{33}$
...
$a_{11} = a_{nn}$
$a_{22} = a_{33}$
...
$a_{22} = a_{nn}$
...
$a_{n-1,n-1} = a_{nn}$
$a_{11} = 0$
...
$a_{nn} = 0$
выделяет в пространстве операторов линейное подпространство коразмерности один. Любое линейное подпространство коразмерности один имеет меру нуль. Объединение конечного числа множеств меры нуль имеет меру нуль.

-- 13.11.2014, 17:48 --

patzer2097 в сообщении #930536 писал(а):

а в 1.6 осталось заметить, что обратимые операторы образуют плотное множество.

Да, точно!

[patzer2097]

1.8. Пока непонятно, причем тут жорданова форма, и как мы перейдем от нее к общему случаю.

[kp9r4d]

patzer2097
Да, что-то я не туда повёл. Не можете дать наводку?

patzer2097 в сообщении #930499 писал(а):

1.3. kp9r4d в сообщении #930484

писал(а):
Единственное собственное значение жордановой матрицы: это $\lambda$. Если $\lambda = 0$ то единственное инвариантное подпространство - подпространство размерности 0. Это неверно, т.к. у жордановой клетки есть собственный вектор..

Да, при любых $\lambda$ есть два инвариантных подпространства: нулевое и $(t,0,...,0)$.

-- 13.11.2014, 19:40 --


-- 13.11.2014, 19:41 --

patzer2097 в сообщении #930499 писал(а):

На самом деле Вы решили задачу полностью - достаточно заметить, что $A$ диагонализируем тогда и только тогда, когда $A+\lambda E$ диагонализируем.

Да, спасибо, это следует из равенства $CAC^{-1} + E = C(A+E)C^{-1}$.

[kp9r4d]

В задаче 1.11 явно же опечатка? Что такое $K[t]/P$ ещё понять можно — фактор по такому-то идеалу, но что такое $K[t]/P \cdot K[t]$?

-- 13.11.2014, 21:04 --

Задача 1.4
Линейное пространство не представимо в виде конечного объединения собственных подпространств.
Решение
Любое линейное подпространство коразмерности $>0$ имеет меру нуль, объединение конечного числа множеств меры нуль имеет меру нуль.

[kp9r4d]

В 1.16, разве не всегда? Если «ревёрснуть» базис, назвав первый базисный вектор последним, второй - предпоследним и т.д. то матрица диагонализируется.

[Xaositect]

kp9r4d в сообщении #930619 писал(а):

В задаче 1.11 явно же опечатка? Что такое $K[t]/P$ ещё понять можно — фактор по такому-то идеалу, но что такое $K[t]/P \cdot K[t]$?

Если $P$ - это многочлен, то $P\cdot K[t]$ - это как раз идеал, порожденный этим многочленом.

[kp9r4d]

Xaositect
Но там-то умножается не на многочлен, а на класс эквивалентности многочленов, именно это и непонятно.

[Xaositect]

kp9r4d в сообщении #930690 писал(а):

Но там-то умножается не на многочлен, а на класс эквивалентности многочленов, именно это и непонятно.

Где? Там фактор кольца $K[t]$ по идеалу $P\cdot K[t]$.

[kp9r4d]

Xaositect
А-а-а. Я просто воспринимал это как-то вроде
$(K[t]/(P)) \cdot K[t]$
тогда понятно, спасибо.