Есть две версии формулы Стокса. Одна более абстрактная в терминах дифференциальных форм, другая (следствие первой) ближе к физике, в терминах потоков вектора, дивергенци и т.д. У студента в голове иногда эти вещи существуют совершенно независимо, особенно если первую формулу рассказывали на матане-дифгеме, а другую в курсе физики. Целесообразно иметь описание этого всего в стандартном формализме дифференциальной геометрии.
Предположим на гладком многообразии

введена форма объема

.
В частности, если в

имеется риманова метрика

то с ней согласована форма объема у которой

.
Пусть

-- гладкое гипермногообразие в

, и

-- векторное поле в

.
Определение. Потоком поля  через поверхность
через поверхность  называется число
называется число  где
где  -- оператор гомотопии, знак перед интегралом ставится в зависимости от того, чего хочет этот физик.
-- оператор гомотопии, знак перед интегралом ставится в зависимости от того, чего хочет этот физик.При наличии метрики это определение превращается в привычное: под интегралом будет стоять единичный нормальный вектор к

скалярно умноженный на

и умноженный на элемент площади на

.
Предположим теперь дополнительно, что многообразие

является границей некоторой ограниченной области

Тогда справедлива следующая версия формулы Стокса.
Теорема.  где
где  -- производная Ли.
-- производная Ли. Заметим, что

Что бы доказать эту формулу напомним формулу гомотопии:

где

-- дифференциальная форма.
И так,

Остается заметить, что
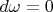
.