Не знаю, насколько следующий алгоритм лучше "лобового", но все же...
Будем обозначать основание системы счисления

, цифру, количество которой необходимо подсчитать

, количество цифр -

.
1. Найдем наибольшее

, при котором все еще справедливо неравенство

(здесь

).
2. Найдем

где

.
3. Найдем количество цифр в записи

в

-ричной системе счисления, не меньших по значению

(обозначим это число

).
Искомое количество цифр

среди первых

символов равно

.
Пример.По условию

,

,

.
1.

, т.к.

2.

,
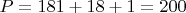
3.

(т.к.

,

)
Итого:

.
Вроде бы, нигде не ошибся... Но для контроля неплохо бы свериться...