Новый раздел математикм

[unnihilator]

Новая наука: "Структурная геометрия".
Основная цель: Ввести в математику, наряду с понятием "число", новое фундаментальное понятие:"структура".
Главная задача: Стать основным звеном математики, связывающим другие ее разделы друг с другом.
Основной инструментарий: " формула реструктуризации (в общем виде): $\int\limits_{x}^{X}f'(x)dx=f(r)$. ( результат применения формулы: $f(r)+f(x)=f(X)$ - читается "$f(r)$ реструктуируется по $f(x)$ в $f(X)$"), правила дифференцирования и интегрирования в "планиметрии" и "стереометрии".
Примеры применения:
$V=\frac{1}{3}\pi r^3$ - без учета структуры;
$V_1=\int\limits_{0}^{x}(\pi r^2)dr=\frac{1}{3}\pi r^3$ - объем конуса (элементарная структура: $\int\limits_{0}^{r} \int\limits_{0}^{r} \int\limits_{0}^{r}(2\pi)d^3r$).

$V_2=\int\limits_{0}^{x}(r)d(\frac{\pi r^2}{2})=\frac{1}{3}\pi r^3$ - объем четверти шара: (элементарная структура $\int\limits_{0}^{r}(r)d[\int\limits_{0}^{r} (\int\limits_{0}^{r}(2 \pi) dr)d(\frac{r}{2})]$).
Используя правила "интегрирования и дифференцирования в планиметрии и стереометрии"
имеем такие результаты (без показа элементарных структур):
$\int\limits_{0}^{r} (2\pi r)dr$ - площадь круга с радиусом "$r$" (эл. стр.: $\int\limits_{0}^{r} \int\limits_{0}^{r}(2\pi)d^2(r))$,

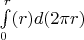
$\int\limits_{0}^{r} (r)d(2\pi r)$ - площадь боковой поверхности конуса высотой "$r$" (эл.стр. $\int\limits_{0}^{r}(r)d(\int\limits_{0}^{r}(2\pi)dr$),

$\int\limits_{0}^{r}(\pi r^2)dr$ - объем конуса высотой "$r$" (эл.стр. $\int\limits_{0}^{r} \int\limits_{0}^{r}\int\limits_{0}^{r} (2\pi)d^3r$),

$\int\limits_{0}^{r}(r)d(\pi r^2)$ - объем полушария с радиусом "$r$" (эл. стр. $\int\limits_{0}^{r} (r)d[\int\limits_{0}^{r} \int\limits_{0}^{r}(2\pi)d^2r]$),

$\int\limits_{0}^{r} (2r)d(\pi r^2)$ - объем шара с радиусом "$r$"(эл. стр. $\int\limits_{0}^{r} (2r)d[\int\limits_{0}^{r} \int\limits_{0}^{r}(2\pi)d^2r]$),

$\int\limits_{0}^{r}(\pi r^2)d(2r)$ - объем двух конусов высотой "$r$", вершинами направленных друг к другу (эл.стр. $\int\limits_{0}^{r} \int\limits_{0}^{r}\int\limits_{0}^{r} (2\pi)d^3(2r)$),


Одним из главных результатов применения этой теории станет очевидным понятие "четвертое измерение пространства по линейной величине" (не путать "четвертое измерение пространства по времени").

[ShMaxG]

Спасибо. Посмеялся.

Добавлено спустя 1 минуту 16 секунд:

... ждите модератора.

[Руст]

Чушь. Пахнет ферматизмом в определённых интегралах.
Был тут один, который не разбираясь в элементарной математике учил математиков математике с помощью своего диалектического материализма и подобной чуши.

[Таня Тайс]

Прощайте, unnihilator

[Виктор Ширшов]

unnihilator в сообщении #193346 писал(а):

Новая наука: "Структурная геометрия".

Зачем геометрии ещё одна "дочь"? Разобраться бы с теми понятиями и формулами, положениями и утверждениями, которыми напичканы элементарная (Евклидова), начертательная, аналитическая, дифференциальная, неевклидова, синтетическая, гиперболическая, эллиптическая геометрии.

[Бодигрим]

Цитата:

- Вовочка, сколько будет шесть плюс четыре?
Вовочка долго молчит. Учитель не выдерживает:
- Но ведь это очень просто. Будет десять.
- Почему? – удивился Вовочка. – Ведь вы вчера говорили, что десять – это семь плюс три!

[xaxa3217]

Ни слова не понял, но, ребят, верить теории 100% можно. Ибо:

unnihilator писал(а):

To gris: Да я в учебники по математике с десятого класса не заглядывал, мне что, делать нечего? Я уже вам писал, вы пропускаете это между ушей: я контачу с информационным каналом. Задаю вопрос - мне отвечают. Отвечают в виде образов. Возможно, из-за моей "неподготовленности" я не совсем так интерпретирую образы. Шредингеру была понятна его формула, потому, что он этой проблемой занимался, Менделееву тоже по этой же причине все стало понятно...

человек контачит с информационным каналом, еще Тесле было известно что это не хухры-мухры.

[Виктор Ширшов]

Руст в сообщении #193359 писал(а):

Чушь. Пахнет ферматизмом в определённых интегралах.
Был тут один, который не разбираясь в элементарной математике учил математиков математике с помощью своего диалектического материализма и подобной чуши.

Предполагаю, что Вы говорите обо мне, но почему в прошедшем времени.
«Вся история науки на каждом шагу показывает, что отдельные личности были более правы в своих утверждениях, чем целые корпорации учёных..., придерживающиеся господствовавших взглядов». Эти слова в середине 20-х годов прошлого века написал коллегам по академии тогдашний авторитет российской науки В. И. Вернадский, прекрасно понимая, как важно прислушиваться к мнению каждого исследователя.
Самым активным участникам этого форума (Руст, AD, Brukvalub и другим), недружелюбно относящимся к любителям, следует знать, что Ферма был юристом, Э. Резерфорд - фермером, Н. Бор - футболистом (игроком сборной Дании), К. Гаусс водопроводчиком, К. Циолковский - учителем. Таких примеров множество.

[id]

Тсс, не вспомнили бы, кем был Эйнштейн!
И Рамануджан. Это ж живые иконы могли бы быть для альтернативщиков, причем самых разных.

[Jnrty]

Jnrty:

unnihilator, Вам было запрещено открывать новые темы, и уже было строгое предупреждение за нарушение этого запрета. Теперь - бан на неделю. В следующий раз будет насовсем.

Prorab:

Бан стал постоянным за двойную регистрацию