Пока что понятно, что при любой комбинации игрушек в корзине №

, в которой в первую корзину положено

игрушек, число вариантов для корзины №

равно
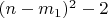
(2 вычитаем (пустое множество и все в

корзине), т.к. обе корзины должны содержать хотя бы

элемент). Например, в куче

игрушек, в первую корзину мы положили

(некий набор из

игрушек, таких наборов всего

(биноминальный коэффициент), то

варианта (приложимых к каждому из первых

вариантов).
-- 08.12.2017, 22:02 --А корзины тоже различимы? Куклу в первую корзину, машинку во вторую — та же самая комбинация, что машинку в первую, куклу во вторую?
Да, корзины не различимы в таком контексте. А даже если бы были различимы, это бы просто умножило результат на

.