Здравствуйте, у меня возникло несколько общих вопросов по перенормировке функций Грина (работаю в физике конденсированного состояния). С перенормировкой сталкиваюсь впервые в работе (не считая учебных курсов в магистратуре, я аспирант).
Для полноты изложения начну немного со стороны.
Исходно у меня есть "голый" двухточечный коррелятор вида
Где

,

-некая скорость.
Затем я хочу перенормировать мою теорию не по схеме Вильсона, а меняя cutoff в реальном пространстве (естественный cutoff у меня связан с постоянной решетки, я его назову

). Я могу написать также уравнение Каллана-Симанчика в виде:
Где моя Бета-функция и аномальная размерность имеют вид (

-константа связи):
Имеем здесь асимптотическую свободу:
Общее решение для уравнения Каллана-Симанчика для нашего случая можно записать в виде (пропущу один шаг выкладок)
Функции

здесь могут быть найдены прямым расчетом коррелятора по теории возмущений. Скажем, в нулевом

(ежели никакого потока нет мы должны восстанавливать свободную теорию в нулевом порядке). Далее, если мы имеем конформную теорию поля на кольце по

-координате, то мы знаем, что в нулевом порядке (сворачивая плоскость в цилиндр):
Соответственно теперь
Мне казалось я это понимаю, пока не надо было обобщать. Возникают следующие вопросы:
1) Я вспоминаю, что коррелятор есть функция двух переменных. Координаты

и времени

. То есть вообще говоря голый пропагатор у меня необязательно "изотропный", моя теория тоже на кольце, и там уже затравочная ФГ имеет вид типа

. Как тогда будет выглядеть RG-step? Мне нужно варьировать по отдельности координату и время при перенормировке? Как тогда перепишется уравнение Каллана-Симанчика? Нужно ли там сохранять логарифмическую производную по

или же писать нечто вроде
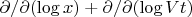
Иными словами, я не понимаю как мне определять "малый масштаб" в теории. Это малые времена, малые координаты, или же малые

?
В целом мне казалось, что неважно как перенормировать теорию вообще... Результат должен быть тот же, но я не понимаю как это показать, пользуясь уравнением Каллана-Симанчика.
2) Вообще мне интересен случай систем конечного размера, когда исходные поля удовлетворяют периодическим граничным условиям (когда я их на цилиндр укладываю, как было выше написано), а еще лучше если открытым (поля зануляются на границе). В любом случае появляется масштаб

-длина системы. Тогда, по идее, я и его могу перенормировать? В чем будет вообще смысл такой перенормировки длины? В статьях люди держат

фиксированным в РГ процедуре, как я понимаю, для удобства?
Или, задам вопрос по-наивному. Каких изменений в РГ-поправках к функции Грина я могу ожидать для системы с периодическими условиями по сравнению с системами с открытыми граничными условиями? Останется ли Бета-функция той же? Просто такое чувство (извините уж за выражение

) что префактор

, что буквально вычисляется через Бета-Функцию и аномальную размерность универсальный в смысле независимости его от граничных условий, которые мы накладываем на поля.
Думаю, это не все вопросы, но начну с них. Спасибо!



