Введение. Причиной моего заблуждения (
topic110006.html) относительно теоремы Кантора (в которую я изначально верил) была мысль, что функция

хоть и растет быстро, но для каждого фиксированного, сколь угодно большого
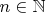
, все же найдется

, такое что

(1), то есть натуральные элементы со скоростью роста

(что соответствует мощности множества всех подмножеств из n элементов) в бесконечной совокупности можно перенумеровать. Но это все же не так.
(1)этот момент, видно, не так очевиден, и не я один спотыкаюсь на нем. Поэтому докажем это строго. Для всякого
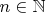
, чтобы было выполнено неравенство

, достаточно положить

. Для конечного

число

в двоичной записи представляет число вида

, имеющее

знак, то есть является конечным натуральным числом. Но если мы перейдем теперь перебором к бесконечности по

и

в неравенстве

, то слева мы получим счетную бесконечность, а справа континуальную. Если бы это был не так, тогда бы теорема Кантора была бы неверна. И множество подмножеств натурального ряда можно было занумеровать натуральными числами.

- мощность множества всех подмножеств.
Позиционно бесконечные числа Каждое (конечное) натуральное число

может быть представлено в

-той позиционной системе счисления в виде конечной линейной комбинации:

, где

– цело число:

. Тогда в m-той позиционной системе счисления оно будет иметь вид конечной последовательности цифр по разрядам.
Расширим данное определение, рассмотрев бесконечные ряды, соответствующие бесконечному набору цифр в позиционной записи, записывая их слева направо, определив позиционно бесконечные числа

, как

, где

– цело число:

. И назовем их

-числа (position numbers), что представляют собой аналог

-адических чисел, где

– любое натуральное число, большее 1.
Сложение и умножением для

-чисел зададим как обычное сложение и умножение в столбик, только слева направо.
Рассмотрим в качестве примера двоичную систему счисления. Тогда

-числа в ней – это счетные последовательности, состоящие из

и

. Сразу отметим, что эти последовательности представляют собой множество всех подмножеств натурального ряда, которые имеют мощность континуума. Также каждому такому набору

-ей и

-ц можно сопоставить вещественную точку на отрезке
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
. А именно этот же набор чисел рассмотреть как двоичное представление вещественных чисел в качестве знаков после запятой. Так

будет соответствовать последовательности

Действительно последняя последовательность представляет собой сумму

.
Зададим отношение порядка, сравнения

-чисел между собой следующим образом. Будем сравнивать их по разрядам слева направо

. Сразу отметим два момента. Если у

-числа начиная с некоторого места имеются одни

-цы, то эти числа легко сравнить с другими такими же: больше то, у которого раньше в разряде начинаются все единицы. Числа, у которых в разряде бесконечно много

, то есть нет места, с которого начинаются все единицы, полагаются заведомо меньшими, чем числа, у которых начиная с некоторого места все единицы. Таким образом самым большим

-числом в двоичной системе счисления будет число, состоящее из одних

-ц:

Это число представляет собой

-адический позиционный ряд

, который равен

. Также заметим, что максимально большое

-число не зависит от основания

и равно также

. А именно, в

-той системе счисления максимальным

-числом будет

Умножив обе части на

, получим

, откуда следует, что

.
Таким образом сложение и умножение не будет выводить

-числа из класса

-чисел, ибо

(максимально большое

-число)

. Такая сумма представляет собой математический коллапс.
Так как максимальное позиционно бесконечное число по значению не зависит от системы счисления, то обозначим его как

(максимальное позиционно бесконечное число), тогда

.
Множество позиционных чисел (конечных и бесконечным) мы будем называть позиционным кольцом и обозначать

. По аналогии с множеством натуральных чисел, представляющих собой натуральную, счетную бесконечность, мы будем говорить о позиционной бесконечности, состоящей из позиционных чисел, но которая уже представляет собой множество мощности континуум.
Введем понятие математического коллапса. Так ныне стала модной теория физического коллапса вселенной, а именно, что наша вселенная, расширяясь, не может расширяться до бесконечности, и, дойдя до некоторого момента, свернется до точки сингулярности, или превратится в черную дыру. Но вот нечто подобное, оказывается, существует в математике.
А именно математическим коллапсом мы назовем сумму обычных единиц, взятом в достаточном количестве, такую, что

. А структуру, имеющую математический коллапс, назовем закольцованной.
Так вот сумма

(просто исчезает на глазах, коллапсируется). Здесь мы на каждом шаге увеличиваем количество слагаемых единиц в соответствии со степенями

-ки. Данная сумма представляет собой математический коллапс. А

-числа оказываются закольцованной структурой. Также это верно для любых m-позиционных чисел. То есть множество

является закольцованным.

-числа являются кольцом. То есть представляют замкнутую структуру относительно сложения и умножения. И для каждого

-числа существует обратный относительно сложения элемент. Так вот

-числа как раз оправдывают название кольца, круга, по существу. А именно, сложение достаточного числа

-ц приводит к тому, что мы начинаем с некоторого момента ходить буквально по кругу.
Понятно, что для кольца вычетов по модулю

, достаточно взять

единиц, которые в сумме равны

. Поэтому кольцо вычетов имеет характеристику

. Характеристика кольца и определяется как целое положительное число. Для

не существует такого целого положительного числа

, что сумма m единиц оказывается равна нулю. Поэтому характеристикой

является

. Но оказывается, что если взять достаточно большое число

-ц, в количестве

, то мы получим

. То есть, если характеристикой кольца считать не целое положительное число, а допускать возможность полагать большие величины, то характеристикой

является величина

.
Почему мы называем позиционно бесконечные числа иногда натурально бесконечно большими числами, потому что их можно складывать как натуральные числа между собой, так и складывать с обычными натуральными числами. Например, 1+11111… = 1+(-1) = 0.
Легко проверить, что p-числа, у которых начиная с некоторого места имеются все 1-цы, представляют собой отрицательные целые числа, то есть -∞ (минус бесконечность). А также те числа, у которых, начиная с некоторого места имеются только 0, представляют собой просто натуральные числа.
Осталось задать порядок между

-числами, в записи которых бесконечно много

-ей и

-ц. Здесь сразу же возникает трудность в сравнении по разрядам, ибо

и

чередуются и это сравнение уходит в бесконечность, то есть возникает некоторая неопределенность. Но! Заметим, что каждому

-числу мы можем сопоставить единственное (!) вещественное число, просто записав всю последовательность цифр, представляющих

-число, после запятой, тогда у нас получится

-ое разложение какого-то вещественного числа. Причем это соответствие будет взаимно-однозначным, то есть между

-числами и вещественными числами на отрезке
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
существует биективное соответствие. А также на отрезке
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
имеется упорядочивание вещественных чисел строго по значению m-ого разложения. Тогда мы можем перенести этот порядок на порядок между

-числами только в обратном соответствии, то есть знак больше заменить на меньше.
Давайте рассмотрим пример:
Возьмем двоичное разложение числа

, что будет соответствовать

-числу


, что представляет сумму с нечетными степенями

.
В дополнение рассмотрим число с четными степенями

.
Тогда
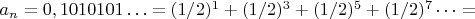

А также заметим, что

Отсюда получаем, что

.
А теперь вычислим соответствующие им

-числа:


И также верно, что

.
Отсюда следует, что

. То есть мы видим, что

.
Можно несложно доказать (и я это проделал), что для любого

, вещественное число на интервале

, имеющее в

-ой системе счисления периодическую запись, по значению в точности равно значению со знаком минус

-ого числа, имеющего в m-ой системе счисления обратный период. А именно: пример, если вещественное число

, то

(сопряженное

-число)

по значению. То есть сопряженные числа оказываются симметричными относительно нуля. И одно из другого получается умножение на

. То есть периодические

-числа имеют дробные значения, которые заключаются на интервале

. То есть континуум значений

-чисел по нецелочисленным значениям располагается где-то на вещественной прямой. И некоторые

-числа с нецелыми значениями оказываются даже больше

, хотя по разрядам они и считаются меньшими.
Так, кстати, по значению

Можно также отметить, что если вещественное число имеет более значимым разряд, ближайший к нулю, левый, то

-числа соответственно более значимым имеют разряд, который располагается правее. Если бы мы могли привести бесконечную запись вещественного числа к единому общему знаменателю, то мы увидели бы обратное соответствие по записям разрядов (то есть если запись зеркально отобразить по разрядам в противоположном порядке). Но в общем случае мне не удалось доказать, что для любого вещественного

из

,

по значению (это, наверное, и не так).
В любом случае, мы имеем такое представление:

-числа, в разряде которых, начиная с некоторого места имеются все

, представляют собой целые отрицательные числа от

до

по значению.

-числа, у которых, начиная с некоторого места имеются все

, это обычные натуральный числа от

до

по значению. Периодические

-числа по значению – это какие-то дробные числа на интервале

. Ну и остаются какие-то непериодические бесконечные наборы

и

, которым можно биективно сопоставить строго упорядоченные вещественные числа на интервале

. Причем эти

-числа будут иметь нецелые значения, ибо у нас уже целые числа заняты. Да и в общем-то нам их упорядочивание по разрядам не значимо.
В целом же представленные ниже формулы имеют смысл, понимая, что выражения слева есть также поворот по оси на

:
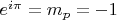

Заметим также, что

. Если положить

, то получим

. А тогда получаем удивительную формулу:

, которую можно записать так:

для любого натурального

.
И что же означает это уравнение, этот математический коллапс? А то, что если у нас есть бесконечная запись какого-то

-числа с бесконечной последовательностью ненулевых цифр, то умножение его на основание просто сдвигает цифры вправо, а бесконечно удаленная цифра пропадает, обращается в ноль. То есть если представить фиксированную бесконечную запись

-числа по цифрам, то умножение его на основание m сдвигает все цифры вправо, а самой бесконечно удаленной цифре ничего не остается, ибо все места заняты, как обращаться в

.
Если мы обозначим бесконечную степень любого натурального числа

как

, то получим, что

или другими словами:

.
То есть

похоже на элемент класса вычетов по модулю

!

есть и ни что иное как бесконечно удаленная

-ца.
Можно даже рассмотреть множество, состоящее из элементов

, что представляет собой кольцо… бесконечно удаленного разряда.
Принимая во внимание, что бесконечно удаленный разряд имеет приоритет над всеми предыдущими разрядами, то число, у которого

- ненулевой бесконечно удаленный разряд, больше тех чисел, у которых он нулевой или имеет значение меньшее

.
Кстати максимальность позиционно бесконечного числа, в записи которого стоят только

цифры – максимальный класс вычета по модулю m, легко проиллюстрировать прибавлением в столбик

-цы, а именно, например, для

:


_________

Поэтому число

мы и назвали максимумом позиционно бесконечных чисел, ибо оно представляет предельно максимальное последнее целое число перед

, а также в разрядной записи имеет все

, то есть по разрядам превосходит все остальные.
Также отметим, что с одной стороны, если позиционно бесконечное число обрезать в любом месте, оно будет представлять обычное натуральное число. С другой стороны, если его не обрезать, то оно будет представлять либо отрицательное целое число, либо какое-то нецелое число по значению. Вместе с тем, количество позиционных чисел континуум, то есть несчетное число. То есть их больше, чем обычная натуральная бесконечность! То есть, если мы будем последовательно отсчитывать единицы в позиционном разложении слева направо, то мы будем получать натуральный ряд чисел, перебирая каждый раз натуральные числа, но если мы рассмотрим бесконечность таких чисел, то получим континуум, а не счетное множество. И связано это с на порядок большей скоростью роста по величине множества всех подмножеств числа n по сравнению с ростом линейной функции n, отсчитывающей по одному разряду. То есть у нас счетное число разрядов, но при этом несчетная величина позиционно бесконечных чисел.
Заметим также, что если мы рассмотрим суммы вида

, где

– произвольные натуральные числа, то у нас возникает неопределенность, связанная с бесконечностью. Это происходит от того, что в таком представлении каждое натуральное число имеет множество вариантов представления. Число вариантов представлений, разбиений натурального числа на составные слагаемые, кстати, дает формула Рамануджана-Харди. А более число композиций – представлений разбиения с перестановками – равно

для любого натурального

.
Пример, рассмотрим ряд

, этот же ряд мы можем записать, например, как

, объединив соседние единицы по две в двойки, что равно

, а тогда

. Противоречие.
Но если мы задаем структуру представления натуральных чисел через

-тую позиционную систему счисления, то каждое натуральное число имеет единственное! представление в виде суммы по степеням

. Это происходит от того, что степенная функция растет на порядок круче линейной, подходя для структурирования бесконечности в связи с тем, что умножение как возведение в степени растет действительно быстрее, чем простое прибавление (ибо перед весами

мы рассматриваем числа

). Так

ровно на

-цу меньше, чем

, вот это равенство и обеспечивает единственность(!) представления натуральных чисел в

-ой системе счисления. Далее мы рассмотрели расширение ряда натуральных чисел позиционно бесконечными числами,

-числами.
С ув. Алексеев Андрей, Андрей Петербургский