Hi,
I would like to verify the sum of energy of this isolated device:

The half disk has a lot of small balls inside. No friction. The mass of the ball is 0 (theory). There are springs that attract balls with the law
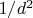
to have the pressure on the walls like gravity can do with water. The mass of the spring is 0. Each spring is attached from the red center to a ball. All the device turns around the red center. The center of the half disk turns too around the red center but it is the black arm that take the black center. Like the centers of rotation red and green are not the same, the black arm must increase its length when it turns, I drawn a cylinder for that. The law of attraction of a spring is
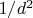
with d the distance from the red center. Note, the springs never lost any potential energy because the balls keep their position in the half disk.
The force F1 come from the pressure on the red wall.
The force F2 come from the pressure on the black center (the pressure to the half circle goes to the black center).
The force F3 come from the springs.
The torque T1 come from F1 around the red center.
The torque T2 come from F2 around the
black center. I calculated
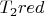
too to verify the sum of torque around the red center is well at 0.
The device turns like that: I calculated the forces and the torques around the red center, I'm not sure about F3x and F3y:
I calculated the forces and the torques around the red center, I'm not sure about F3x and F3y:I don't take in account the sign of the value
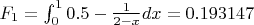
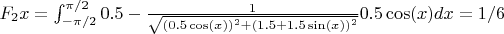
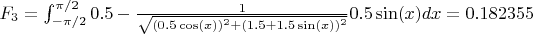
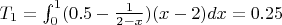
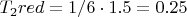
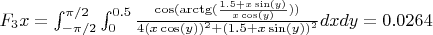
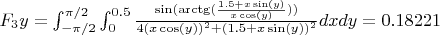

The sum of forces is well at 0. The sum of torques around the red center is well at 0.
The torque T2 around the black center and the energy:I noted

is the angle of rotation of the red arm (clockwise), in this case the black arm turns of
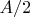
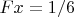
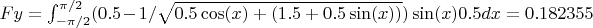
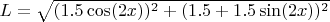
I need to have

inside trigo functions because when I integrate I do from 0 to
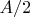
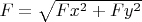
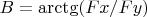
Torque

around the black center:
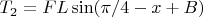
Energy recover from black arm:
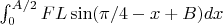
Energy needed to increase the length of the black arm:
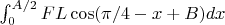
Energy needed from red arm:
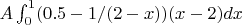
The sum of energy for an angle A:
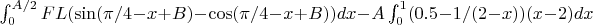
But the result is not 0, it is
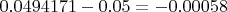
. The difference is small but it is not 0 because the integration take the force with a factor

but the length change with square root of

. So, I think I made a mistake about an angle. If you can help me please ?
++