Физический смысл векторного произведения

[Nesalvador]

Евгений Машеров в сообщении #1053246 писал(а):

Ну, скалярному произведению найти физический смысл нетрудно...

А не подскажете ли,

физический (природный, что ли) смысл (или "обоснование", как в этой теме было названо) векторного перемножения векторов?

Я не математик, и не физик, но мне необходимо понять - почему вектор момента импульса и момента силы направлен перпендикулярно плоскости всех действий при стандартных условиях?
Это направление исходит из правила векторного перемножения векторов: радиус-вектора и силы (как пример для момента силы) -- поэтому вопрос пишу здесь, а не в разделе физики.

[Munin]

На самом деле, "векторное произведение векторов" - это упрощение от более сложной операции: внешнего произведения. Чтобы ради одной этой операции не вводить ещё 1-2 разновидности геометрических объектов, с правилами работы с ними. У такого внешнего произведения тоже есть направление, взаимно однозначно связанное с направлением вектора: внешнее произведение имеет направление в плоскости, которой перпендикулярен вектор. И эта плоскость - это есть плоскость "всех действий".

Поэтому, вектор-результат в векторном произведении (в физических случаях) - это просто условность.

[arseniiv]

Угу. Как вектор можно проиллюстрировать направленным отрезком, так и би-, три-, …, поливектор — внешнее произведение нескольких векторов — иллюстрируется «направленной» площадкой, объёмом и т. д.. Направление площадки можно изобразить направлением вращения в ней — ↻ или ↺ (и смотря откуда смотреть на неё, конечно). Направление объёма уже лично я не умею пока представлять, но можно направление $(n+1)$-объёма согласовать с направлениями его $n$-мерной поверхности. Например, на гранях кубика или на сфере можно нарисовать ↻ или ↺ так, чтобы перенос их по поверхности с одного места на другое давал одно и то же, и это можно сделать только двумя способами и сопоставить направлениям того, чья была поверхность.

В трёхмерном пространстве все аксиальные векторы имеют какую-то связь с вращением, и более натурально она видна, как уже сказал Munin, если заменить векторное произведение $\times$ на внешнее $\wedge$, и аксиальные векторы, соответственно, на бивекторы, определяющие плоскость, направление и «количество» (это ведь не всегда угол, см. угловую скорость) соответствующего вращения.

В высших размерностях дела становятся интереснее, а аксиальные штуковины — натянутее: в четырёхмерии:
• Вращению соответствует уже аксиальный бивектор (не тот же самый, что «естественный» бивектор, описывающий плоскость вращения — этот ему всё так же ортогонален).
• Вращение может происходить в нескольких плоскостях одновременно.
• Потому бивектор описывает уже не обязательно одну площадку. Пусть у нашего пространства есть базис из векторов $\vec\imath,\vec\jmath,\vec k,\vec\ell$, тогда бивектор $a\vec\imath\wedge\vec\jmath + b\vec k\wedge\vec\ell$ — это «сумма» площадок, построенных на $\vec\imath,\vec\jmath$ и $\vec k,\vec\ell$ площадей $a$ и $b$; в трёхмерии такой не составишь — там любой бивектор можно привести к виду $\vec u\wedge\vec v$.
В размерностях больше 4 аксиальное описание вращения уже получается поливектором более высокой степени, чем два. В камин его.

[Munin]

arseniiv в сообщении #1087348 писал(а):

Направление объёма уже лично я не умею пока представлять, но можно направление $(n+1)$-объёма согласовать с направлениями его $n$-мерной поверхности.

По сути, направление любого $n$-мерного объёма - это упорядочение его $n$ базисных векторов. Любой другой базис имеет либо ту же ориентацию, либо противоположную, так что направление от конкретного базиса не зависит.

Например, направление площадки, изображаемое $\circlearrowleft,$ - это направление, задаваемое порядком $(\mathbf{i},\mathbf{j}),$ или буквами $Oxy,$ если так понятнее. А противоположное направление $\circlearrowright,$ - соответствует $(\mathbf{j},\mathbf{i}),$ или $Oyx.$ Или, разумеется, что то же самое, $(\mathbf{i},-\mathbf{j}).$

Теперь, надеюсь, понятнее, как это переносится на бо́льшие размерности.

arseniiv в сообщении #1087348 писал(а):

если заменить векторное произведение $\times$ на внешнее $\wedge$

Что интересно, во Франции векторное произведение так и обозначается $\wedge,$ по крайней мере в Википедии :-)

[Евгений Машеров]

Поскольку математическое объяснение уже дано, и куда более компетентными меня людьми, но вопрос был изначально обращён ко мне, то ограничусь советом купить гироскопический кистевой тренажёр и поиграть с ним. Ощущая рукой существование сил, действующих "под прямым углом".

[arseniiv]

(Оффтоп)

Munin в сообщении #1087356 писал(а):

По сути, направление любого $n$-мерного объёма - это упорядочение его $n$ базисных векторов.

Если написать так, не очень хорошо получается. Направлений всегда два, но $n! = 2$ только при $n = 2$. Т. е. понятно, что связь с порядком «внешних множителей» остаётся: два мультивектора, полученные из одних и тех же множиелей, имеют одинаковую ориентацию, если перестановка множителей первого произведения в множители второго чётная — наверно, вы это и хотели сказать?

[Munin]

(Оффтоп)

Евгений Машеров в сообщении #1087364 писал(а):

и куда более компетентными меня людьми

Чтоб я умел так выражаться!

-- 31.12.2015 20:52:29 --

(Оффтоп)

arseniiv в сообщении #1087369 писал(а):

Если написать так, не очень хорошо получается.

Да, если зафиксировать набор векторов, то ориентация будет воспроизводиться при чётных перестановках этого набора. Но обратите внимание, что можно брать и другие векторы. Например, можно заменить в заданном наборе векторов знаки у $k$ векторов, и ориентация изменится, если $k$ нечётное, и сохранится, если чётное.

В общем, дать точную и строгую формулировку, как я понимаю, - то же самое, что дать точное определение самого внешнего произведения. А это скучно, отсылаю к Википедии.

[Cos(x-pi/2)]

Nesalvador в сообщении #1087327 писал(а):

Я не математик, и не физик, но мне необходимо понять - почему вектор момента импульса и момента силы направлен перпендикулярно плоскости всех действий при стандартных условиях?

Nesalvador
Полагаю, это можно понять, пристально разглядывая рисунки с вращающимися телами. Например, пусть два шарика (точнее говоря, две материальные точки $P$ и $P'$) с одинаковыми массами $m$ вращаются по инерции, скреплённые невесомым жёстким стержнем. Для 3-мерности рисунка изобразил ещё и плоскость с круговой орбитой шаров в виде поверхности стола, хотя никакого стола в этом примере нет :)



Здесь ось вращения очевидным образом перпендикулярна плоскости орбиты, т.е. в каждый момент времени ось вращения перпендикулярна вектору скорости шара $\vec{v}$ и перпендикулярна радиус-вектору шара $\vec{r} = \overrightarrow{OP},$ проведённому из середины стержня $O$ (будем следить за шаром $P,$ а для второго шара всё будет аналогично). При этом в каждый момент времени векторы скорости перпендикулярны радиус-векторам шариков.

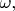
Наличие оси вращения люди условились выражать вектором угловой скорости $\vec{\omega}.$ Величина его равна угловой скорости вращения $\omega,$ а его направление символизирует направление оси вращения. Более строго говоря, вектор угловой скорости это псевдовектор (его также называют аксиальным вектором): "начало" и "конец" на оси вращения выбраны условно - так, чтобы глядя с "конца" вектора $\vec{\omega}$ мы видели вращение против часовой стрелки.

Какой формулой выражается взаимосвязь векторов $\vec{\omega},$ $\vec{v}$ и $\vec{r}$? Сначала найдём связь между числовыми величинами этих векторов. Если шар движется по круговой орбите с постоянной скоростью $v,$ то всю длину окружности $2\pi r$ он проходит за время $T=2\pi r/v$ - за это время шар совершает один орбитальный оборот, т.е. поворачивается вокруг точки $O$ на угол $2\pi.$ Значит, величина орбитальной угловой скорости, определяемая как $\omega=2\pi /T,$ есть $\omega = v/r.$ Эту же взаимосвязь числовых величин можем описать равенством:

$v=\omega r \qquad (1)$

А для того, чтобы из такой формулы была видна не только указанная связь величин, но и направления векторов относительно друг друга, запишем вместо (1) следующее векторное равенство с символом векторного произведения $\times$

$\vec{v}=\vec{\omega} \times \vec{r} \qquad (2)$

Мы условимся здесь, что направление векторных сомножителей и векторного произведения друг относительно друга именно такое, какое показано выше на рисунке; все три вектора там взаимно перпендикулярны. Если представить себе ещё один шарик - в виде материальной точки расположенной на оси вращения первых двух шаров над (или под) плоскостью их орбиты, - то его скорость $\vec{v}=0,$ а радиус-вектор параллелен $\vec{\omega}.$ Значит, векторное произведение (2) взаимно параллельных (или антипараллельных) векторов равно нулю.

Можно заметить также, что если изобразить новую картинку, где на месте прежнего вектора $\vec{\omega}$ будет нарисован новый $\vec{r}$, а на месте прежнего $\vec{r}$ будет новый $\vec{\omega},$ то новая скорость $\vec{v}$ окажется противоположной к прежней; значит, векторное произведение меняет свой знак при перестановке сомножителей:

$\vec{\omega} \times \vec{r} = - \vec{r} \times \vec{\omega} \qquad (3)$

Очевидно также, что если в прежней плоскости орбиты включить на короткое время $dt$ пару противоположных сил, которые увеличат (или уменьшат) скорость $v$ показанных выше двух шаров, то увеличится (или уменьшится) угловая скорость шаров $\omega$, а направление оси вращения останется прежним. Т.е. вектор угловой скорости $\vec{\omega}$ удлинится (или укоротится) на какой-то вектор $\vec{d \omega}$ без изменения своего направления. Этот факт ведёт нас к представлению о некоем "векторе момента сил", вызывающем изменение $\vec{d \omega}$ вектора угловой скорости $\vec{\omega}$. В данном примере естественно думать, что вектор момента сил параллелен оси вращения, поскольку вызванное им изменение $\vec{d \omega}$ параллельно оси вращения. Попробуем это записать в форме векторного равенства.

Представим себе вектор силы $\vec{F},$ параллельный вектору скорости $\vec{v}$ шара $P.$ За короткое время $dt$ сила изменяет вектор импульса шара $\vec{p}=m\vec{v}$ на

$\vec{dp} = \vec{F}dt,$

так что (это второй закон Ньютона):

$\dfrac{\vec{dp}}{dt} = \vec{F} \qquad (4)$

Чтобы представить это равенство как равенство векторов, параллельных оси вращения шаров, умножим векторно левую и правую сторону этого равенства на радиус-вектор шара $P:$

$\vec{r} \times \dfrac{\vec{dp}}{dt} = \vec{r} \times \vec{F} \qquad (5)$

Обозначив здесь левую сторону как $\vec{dl}/dt$ - это у нас будет вектор скорости изменения "момента импульса", а правую сторону обозначив как $\vec{K}=\vec{r} \times \vec{F}$ - это у нас будет вектор "момента сил", можем записать равенство (5) в виде:

$\dfrac{\vec{dl}}{dt} = \vec{K} \qquad (6)$

В качестве не сильно сложного упражнения проверяется, что при этом сам орбитальный момент импульса материальной точки $P$ можно определить формулой:

$\vec{l}=\vec{r} \times \vec{p} \qquad (7)$

В нашем примере орбитальный момент импульса одного шарика-точки есть $\vec{l}=mr^2\vec{\omega}.$ Система двух шариков $P$ и $P'$ имеет вдвое больший момент импульса.

Рассмотрим теперь другую ситуацию. Пусть до включения пары сил шарики $P$ и $P'$ покоились, а затем на короткое время включалась пара сил, перпендикулярных той же плоскости, которая была показана на предыдущем рисунке:



Очевидно, что здесь за время $dt$ шарики приобрели угловую скорость $\vec{d\omega}$ в направлении "на нас". Соответствующее этому факту изменение момента импульса одного шарика есть

$\vec{dl} = \vec{r} \times \vec{F}dt,$

где $\vec{dl} =mr^2\vec{d\omega}.$

Наконец, можем попытаться "просуммировать" эту ситуацию с самой первой ситуацией, где шарики вращались вокруг вертикальной оси (см. первый рисунок). Мы видим, что показанная на втором рисунке пара сил стремится повернуть стержень в плоскости рисунка, т.е. эта пара сил как бы "стремится наклонить ось вращения налево". Однако, векторы $\vec{\omega}$ и $\vec{l},$ параллелльные вертикальной оси вращения, при этом получают добавки $\vec{d\omega}$ и $\vec{dl},$ направленные "на нас", и превращаются в слегка наклонённые "на нас" векторы $\vec{\omega}+\vec{d\omega}$ и $\vec{l}+\vec{dl}.$

(С Новым Годом!)

(Если чё-ньть слегка напутал, прошу извинить, всё ж таки Новый Год. Всех с Новым Годом! :-)

[arseniiv]

Кстати о напутанном: я вчера некорректно написал

arseniiv в сообщении #1087348 писал(а):

оливектор — внешнее произведение нескольких векторов

и потом дальше же показал на неразложимый бивектор

arseniiv в сообщении #1087348 писал(а):

$a\vec\imath\wedge\vec\jmath + b\vec k\wedge\vec\ell$

Поправляюсь. Поливектор может быть суммой подобного вида многих произведений одинакового числа векторов. Точнее и аккуратнее это будет, как уже упомнил Munin, если смотреть определение внешней алгебры.

Это для точности просто.

[Munin]

Добавлю одно неочевидное и не очень приятное обстоятельство:
Векторное правило сложения $\vec{\omega}+d\vec{\omega}$ работает только для угловых скоростей, но не для самих углов вращения! Это отличается от ситуации с невращательным движением, где сложение выполняется и для радиус-векторов $\vec{r}+d\vec{r},$ и для всех их последующих производных по времени: $\vec{v}+d\vec{v},$ $\vec{a}+d\vec{a}.$ Для угловых скоростей, записывать правило сложения можно, и дифференцировать его можно (сколько угодно раз), а вот "интегрировать" и записывать аналогичное правило для углов поворота - нельзя!

Математически, существуют реальные и точные формулы для сложения углов поворота, но они оказываются более сложны, и увы, выходят за рамки векторной алгебры. Сложение углов поворота неперестановочно, и выражается матричным произведением. Из-за этого, оно обычно вообще не излагается в общем курсе физики, хотя его можно найти в более математизированных курсах.

[Утундрий]

Munin в сообщении #1087425 писал(а):

существуют реальные и точные формулы для сложения углов поворота, но они оказываются более сложны, и увы, выходят за рамки векторной алгебры

Если вы о формуле поворота Родрига, то интересно было бы узнать, каким образом она выходит за рамки векторной алгебры?

[Munin]

Нет, я не про неё, я про $\mathrm{SO}(3).$ Опять у вас какие-то левые ассоциации типа "музыкой навеяло", на основании которых вы пытаетесь ругаться с окружающими.

[Утундрий]

Ещё раз...

Munin в сообщении #1087425 писал(а):

Математически, существуют реальные и точные формулы для сложения углов поворота, но они оказываются более сложны, и увы, выходят за рамки векторной алгебры. Сложение углов поворота неперестановочно, и выражается матричным произведением. Из-за этого, оно обычно вообще не излагается в общем курсе физики, хотя его можно найти в более математизированных курсах.

В действительности, формула для сложения углов поворота "не выходящая за рамки векторной алгебры" известна с 1840 года.

[Munin]

Формула Родрига не есть формула сложения углов поворота. Спасибо и всего наилучшего.

[Утундрий]

А, ну да, это же так сложно - получить из неё требуемую композицию двух поворотов... Что же, кушайте на здоровье, проповедуйте дальше.