Допустим, мы имеем тензор

- полностью антисимметрический, все индексы нижние. Тогда на языке дифформ мы имеем дифформу

Ранг тензора называется степенью формы. Любая операция с дифформой включает в себя обязательную антисимметризацию, чтобы потом получить снова полностью антисимметрический тензор.
Операции:
- внешнее произведение
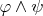
- определяется как
![$\varphi_{[i\ldots j}\psi_{k\ldots l]}$ $\varphi_{[i\ldots j}\psi_{k\ldots l]}$](https://dxdy-01.korotkov.co.uk/f/c/e/6/ce6fae854de6e7389be0195790069e2e82.png)
- внутреннее произведение с вектором

или

- определяется как

- внешний дифференциал

или

- определяется как
![$\partial_{[i}\varphi_{j\ldots k]}$ $\partial_{[i}\varphi_{j\ldots k]}$](https://dxdy-01.korotkov.co.uk/f/8/b/4/8b4a950e2340ae9a20e828de88f6546882.png)
- сопряжение (звезда) Ходжа

или

- определяется в разных текстах по-разному:

либо: с множителем

либо: с верхними, а не нижними, индексами.
Сопряжение Ходжа переводит

-форму в

-форму (или поливектор), за счёт того, что у них одинаковое количество независимых компонент. В частности, оно сопоставляет 3-мерные 2-формы и векторы (возникающие в векторном произведении, то есть, псевдовекторы).
Специальные обозначение:
- дифформы очень любят обозначать буквой
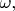
но иногда это произвольная форма, а иногда какая-то специальная - будьте осторожнее; вообще, греческими буквами
- базисные 1-формы

- это базисные ковекторы (тензоры ранга

) вида

- базисные векторы

Обозначение

мотивировано тем, что если взять скалярную функцию

(которая является 0-формой), и от неё внешний дифференциал

(который будет попросту градиентом), то как раз и получится нужный базисный ковектор.
Обозначение

мотивировано тем, что произведения

прочитанные "обычным" способом, дают тот же результат, что и прочитанные в смысле нотации дифформ.
Для

-форм базисными являются формы вида

Дифформа

называется замкнутой, если

Дифформа

называется точной, если существует другая дифформа

такая что


всегда.
Всякая точная форма является замкнутой; обратное вообще говоря неверно, и зависит от топологии области (здесь есть связь с когомологиями).
Любая форма может быть разложена в сумму

- разложение Ходжа, аналог разложения Гельмгольца.
----------------
Интеграл
от дифформы считается корректным только тогда, когда это интеграл от

-формы по

-мерному многообразию (или подмногообразию). То есть, 1-формы можно интегрировать по линиям, 2-формы - по поверхностям, и так далее. Такой интеграл не зависит от введённых координат на многообразии (чем дифформы и удобны, по сравнению с остальными тензорами). Интеграл записывается в несколько непривычном виде:

но если расписать подынтегральную форму через базис, то получится нечто более знакомое:

где

- скалярная функция, а

- элемент соответствующего многообразия (линии, поверхности и т. п.), ориентированный.
Обобщённая теорема Стокса:

где

обозначает край (границу) многообразия
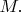
----------------
Про производную Ли, ковариантную производную и пуллбэк не напишу.
-- 10.09.2015 00:19:22 --Munin, а вы не можете подсказать, где про эти дифформы прочесть, чтоб не особо углубляться.
Кроме названных, вспомнил ещё
Арнольд. Мат. методы класс. механики.И наоборот, если хочется все зубы обломать.
Сарданашвили. Современные методы теории поля. Т. 1. Геометрия и классические поля.Ну, почему сразу - пошлость.
Ну потому что это, всё-таки, не Зорич :-)
Кроме того, там дано даже меньше минимума. Теорема Стокса, и всё.