Да нет, определение-то как раз много места не займёт, только, боюсь, толку от него не будет - с ним работать надо.
Пусть

. УМО
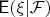
- это случайная величина

(любая из) со следующими свойствами:
(1)  измерима относительно сигма-алгебры
измерима относительно сигма-алгебры  ;
;
(2) Для любого события 
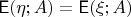
(математические ожидания по множествам).
Соответственно,
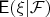
отличается от
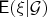
хотя бы первым пунктом.
Если на пальцах, имея в виду величину

с конечным
вторым моментом, то УМО
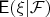
есть проекция в гильбертовом пространстве случайных величин со скалярным произведением
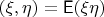
случайной величины

на линейное пространство случайных величин, измеримых относительно сигма-алгебры

. Соответственно,
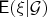
- проекция той же величины на линейное пространство случайных величин, измеримых относительно сигма-алгебры
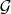
. Вот и разница.
Да и вообще - в русском разделе вики неплохо написано
то же самое.