В моей теме
topic94091.html описан алгоритм определения остатков от числа

, взятого по последовательным модулям.
Рекуррентная форма записи алгоритма деления положительного целого числа

на последовательные модули

:


, тождественно равно модулю

но используется в качестве обозначения основания системы счисления в которую переводится число

при взятии его по модулю



и

старший и младший разряды числа взятого по


(

).

- принимает целые значения 1,2,3... Это единица переноса в старший разряд из младшего в тот момент, когда младший разряд (в результате пошагового накопления) превысил

- вес младшего разряда.

вычитается из

пока

остается положительным. Максимальное количество вычитаний и будет составлять "единицу переноса" равную

Из алгоритма непосредственно вытекает формула восстановления числа

по двум последовательным остаткам:

откуда:

Имеем систему уравнений:



-целая часть [

],

- остаток от деления

(простите, строгого математического описания, оформления остатков я не нашел)

-целая часть[

],

- остаток от деления

решаем систему относительно числа

:

В реальных устройствах редко применяют восстановление

по двум остаткам . Это связано с ограничением для числа

Китайской теоремой

, что ограничивает диапазон вычислений. Поэтому,
для

и

строим идентичную систему уравнений.
Совпадение результата вычислений для

в допустимом числовом диапазоне и будет искомым числом

В данном алгоритме отсутствует операция деление, которая является бичом модульных вычислений.
Строго говоря, из приведенного способа восстановления числа

по остаткам не следует то, что для восстанавливаемого числа

существуют ограничения , определенные в Китайской теореме, а именно то, что

,
и восстановление числа

зависит только от правильного подбора параметра

. Выше приведенный способ, учитывающий ограничения Китайской теоремы , это , думаю, один из способов нахождения единственно правильного

.
Иначе говоря , алгоритм позволяет восстанавливать исходное

по остаткам при взятии их по модулям.
Алгоритм детерминирован, в сторону вычисления остатков, но имеет варианты при восстановлении исходного числа

по остаткам, в узлах появления единицы переноса в старшие разряды. На участках алгоритма, на которых нет подобного переноса, возможно, однозначное восстановление числа

по одному остатку (при фактическом отсутствии ограничений, наложенных Китайской теоремой).
Существует несколько формулировок Китайской теоремы об остатках. Мое предложение
сформулировать возможность восстановления конкретного значения полинома, многочлена по младшему их разряду и весам каждого разряда.
При переводе числа

в иную систему счисления число представляется в виде значений полинома у которого младший разряд является остатком от деления новой СС на его новое основание. Вес каждого разряда числа переведенного в новую СС определяется степенью основания системы счисления.
с основанием СС

В общем виде:
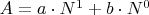
Алгебра многочленов глубоко проработана. Перед ней можно ставить любую задачу, в том числе вопрос о восстановлении всех его разрядов, если известна только часть разрядов, например, младшие и вес остальных.