Ничего не понял. Объясните, что такое стратегия второго игрока. Она каким-то образом должна определять его поведение. Т.е. выбор чистой стратегии обоими игроками (для первого - это просто загадывание числа) полностью определяет ход игры.
-- Вс мар 15, 2015 21:07:38 --
То есть чистая стратегия второго игрока -- это некоторый набор правил, который говорит, в такой-то ситуации называй такое-то число.
Для примера возьмём наименьшее нетривиальное n=3. Ещё раз картинка оптимальных стратегий:
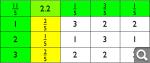
Стратегии второго игрока идут начиная с третьего столбца.
первая стратегия {3, 1, 2} - её нужно использовать с вероятностью 2/5.
{3, 1, 2} значит, что начинаем отгадывать с числа 1, если не угадали выбираем 3, а потом 2. Т.е. алгоритм такой - на первом шаге ищем максимальное число в векторе, который описывает стратегию, его позиция в векторе - это число, которое мы называем. Если не угадали, то на следующем шаге повторяем эту операцию на оставшейся части вектора-стратегии.