Скажите пожалуйста, что можно делать со знаком интеграла?
Чем более старший курс, тем больше вещей, которые с ним можно делать.
В "элементарном" анализе интеграл рассматривается как неделимый символ:

В более продвинутых разделах анализа вводятся разные обобщения этого понятия и этой нотации.
Например, вводится понятие меры, и в качестве "дифференциальной части" записывается какая-то мера:

Или, вводится аппарат дифференциальных форм, для которых

- это оператор, действующий на
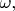
и превращающий форму в форму. Тогда становится возможным записать нечто вроде

и выполнять справа от символа интеграла любые алгебраические операции. Символ интеграла становится одним из многих операторных символов, приписываемых слева.