Работа и энергия

[integer]

В какой книге лучше всего для понимания рассказывается про работу, энергию, консервативные и неконсервативные силы, поле силы? Интересует только ньютоновская механика. ВУЗ технический.

[Sicker]

Савельев

[integer]

Sicker в сообщении #955543 писал(а):

Савельев

Читал, но почему-то не понравилось изложение этих тем.

[nestoronij]

Цитата:

Савельев
Читал, но почему-то не понравилось изложение этих тем.

Смотря какой год издания. После 1989 г. (293 стр.) всё сокращенно и учебник стал ни то ни сё. Самое лучщее издание ( всего 508 стр. т № 1) 1970 г. Но, это моё мнение. Хорошо ещё в К.А. Путилов 1963 г. Несмотря на древность, всё доступно и понятно.

[integer]

Можно примеры нестационарных силовых полей и примеры нецентральных полей?
Потенциальным может быть только центральное стационарное поле или необязательно?
Что такое внешнее поле сил?

[integer]

Закон сохранения энергии выполняется только для замкнутой консервативной системы или для незамкнутой тоже выполняется?

[zvm]

integer в сообщении #955728 писал(а):

Можно примеры нестационарных силовых полей и примеры нецентральных полей?

Электрическое поле в конденсаторе, включенном в цепь переменного тока.

integer в сообщении #955728 писал(а):

Потенциальным может быть только центральное стационарное поле или необязательно?

Не обязательно.

integer в сообщении #955728 писал(а):

Что такое внешнее поле сил?

Поле, созданное источниками, не входящими в рассматриваемую систему.

integer в сообщении #955773 писал(а):

Закон сохранения энергии выполняется только для замкнутой консервативной системы или для незамкнутой тоже выполняется?

Только для замкнутой. Консервативность не обязательна. В консервативной выполняется еще и закон сохранения механической энергии.

[Munin]

Это настолько простые темы, что их можно читать по любому учебнику из любого цикла "курс общей физики". Если у вас после какого-то учебника не всё понятно, то лучше задавайте конкретные вопросы.

integer в сообщении #955728 писал(а):

Можно примеры нестационарных силовых полей и примеры нецентральных полей?

Нестационарное силовое поле:
- возьмём пружинный маятник, и будем произвольно двигать его точку подвеса (задав функцию $x_0(t)$). Груз этого маятника будет находиться в нестационарном силовом поле (силы упругости, поле одномерное).
- возьмём конденсатор, и подадим на него переменное напряжение (опять, задав функцию $U(t)$). Заряженная частица в промежутке между обкладками этого конденсатора будет находиться в нестационарном силовом поле.

Нецентральное поле: возьмём электрический диполь (два заряда, равных по величине и противоположных по знаку), зафиксированный где-то в пространстве. И возьмём пробный электрический заряд. Этот заряд будет находиться в нецентральном силовом поле.

integer в сообщении #955728 писал(а):

Потенциальным может быть только центральное стационарное поле или необязательно?

Не обязательно. Вообще понятие потенциальности независимо и от центральности, и от стационарности.

Потенциальность - это свойство, которое требует знания математического анализа функций нескольких переменных (эта глава называется векторный анализ). Проходится обычно на 2 курсе. Идея такая:
1) Если мы имеем действительную функцию $f(x,y,z),$ то мы можем взять от неё три частные производные по трём аргументам (координатам пространства): $\dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y},\dfrac{\partial f}{\partial z}.$ Предполагаем, что все три производные существуют, то есть, функция $f(x,y,z)$ "достаточно хорошая" для этого.
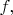
2) Эти три частные производные можно представить себе как три координаты вектора, который называется градиентом функции $f,$ то есть, в некоторой заданной точке
$\operatorname{grad}f=\biggl(\dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y},\dfrac{\partial f}{\partial z}\biggr)=\vec{\imath}\,\,\dfrac{\partial f}{\partial x}+\vec{\jmath}\,\,\dfrac{\partial f}{\partial y}+\vec{k}\,\dfrac{\partial f}{\partial z}.$
Поскольку в другой точке это будет другой вектор, то вообще градиент образует тоже функцию от аргументов $x,y,z$ - векторную функцию, или что то же самое, векторное поле. Её можно представить себе как "стрелки" (векторы), расставленные в пространстве (каждая в какой-то точке).
3) Можно задать какую-то произвольную векторную функцию $\vec{v}(x,y,z),$ но далеко не всегда она будет градиентом от какой-то соответствующей действительной (скалярной) функции. Наоборот, можно сказать, что это будет происходить крайне редко. В этом отличие градиента от обычной одномерной производной: чтобы найти исходную функцию при взятии производной, нужно просто проинтегрировать результат и всё. А с градиентом это срабатывает редко. Вот такие векторные функции, которые всё-таки являются градиентами скалярных, называются потенциальными векторными полями. А остальные - непотенциальными.

Подробно о критериях потенциальности векторного поля написано в учебнике матанализа, а здесь скажу, что например, если "стрелки" образуют замкнутое колечко, то такое векторное поле - непотенциальное.

integer в сообщении #955728 писал(а):

Что такое внешнее поле сил?

Понятия не имею. Может быть, поле внешних сил?

-- 03.01.2015 16:28:01 --

integer в сообщении #955773 писал(а):

Закон сохранения энергии выполняется только для замкнутой консервативной системы или для незамкнутой тоже выполняется?

Для незамкнутой тоже (была бы она только консервативной), но формулируется в другом виде: надо учитывать энергию, переданную в систему или из неё наружу.

[integer]

Munin в сообщении #955782 писал(а):

Может быть, поле внешних сил?

Да.

-- 03.01.2015, 16:38 --

А почему для того, чтобы система была консервативной, внешние потенциальные силы должны быть стационарными?

[Munin]

integer в сообщении #955787 писал(а):

А почему для того, чтобы система была консервативной, внешние потенциальные силы должны быть стационарными?

Упс. Что-то объяснение в двух словах в голову не лезет. Я знаю, где это написано: ЛЛ-1 глава 2 "Законы сохранения", но вот рассказать на пальцах... извините, я сейчас не в форме.

[Oleg Zubelevich]

в теорему об изменении энергии системы входят все силы и внешние и внутренние причем равноправно. поэтому не очень понятно зачем ввводить в этом контексте подразделение сил на внешие и внутренние.

[Ascold]

Цитата:

А почему для того, чтобы система была консервативной, внешние потенциальные силы должны быть стационарными?

"На пальцах" приходит в голову следующее: если потенциальные силы нестационарны, т.е. соотв. потенциальные энергии зависят от времени явно, то градиент потенц. энергии, умноженный на вектор б.м. перемещения(работа потенциальной силы) будет не равен полному дифференциалу потенц. энергии(отличаются на слагаемое $U'_tdt$), что не позволяет написать $dA=-dU$.

[amon]

Ascold в сообщении #956768 писал(а):

если потенциальные силы нестационарны, т.е. соотв. потенциальные энергии зависят от времени явно

Довольно легко придумать пример, когда потенциальная энергия от времени зависит, а силы - нет. (Правда, не знаю, уместно ли это здесь, или только запутает несчастного ТС). При этом потенциальная энергия, естественно, будет зависеть от скорости.

[Munin]

amon в сообщении #956817 писал(а):

При этом потенциальная энергия, естественно, будет зависеть от скорости.

Эээ, а разве это в "школьном" изложении вообще потенциальной энергией называется?

[amon]

Munin в сообщении #956836 писал(а):

Эээ, а разве это в "школьном" изложении вообще потенциальной энергией называется?

А пес ее знает. Энергию взаимодействия заряда с магнитным полем вроде в школе "проходят".