Здравствуйте!
Правильно ли я подсчитал вероятности I, II, III, IV и V?
Подробности ниже.
Рассматривается вопрос об оценке вероятности причин дефектов в телефонных звонках абонентов сотовой связи при функционировании базовых приемопередающих станций (БППС) в определенный конечный промежуток времени.
Предполагается, что известны числа

, где

– общее количество БППС в сети оператора,

- общее количество звонков поступивших в

-ю станцию,

- количество дефектных звонков среди поступивших в

-ю станцию.
Предполагается, что

,

.
Введем следующие обозначения:

- тотальное количество звонков,

- тотальное количество дефектных звонков,

- тотальная доля дефектных звонков,

- доля дефектных звонков при обслуживании

-ой станцией.
Рассмотрим следующие случайные события:

- наугад выбираемый звонок из поступивших окажется дефектным;

- наугад выбираемый звонок из поступивших обслуживался

-ой станцией,

.
Каждый звонок (входящий или исходящий) в каждый момент времени обслуживается одной станцией. Следовательно, события

,

образуют полную систему несовместных событий.
Все причины дефектов разделены на взаимоисключающие типы - события

, где

– общее количество типов. Таким образом, дефектный звонок случается тогда и только тогда, когда происходит одно из событий

. Следовательно, события

,

образуют полную систему несовместных событий.
Пусть
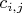
– количество дефектов на

-й БППС по причине

, то есть в случае события

. Тогда для количества дефектных звонков

на

-й БППС имеет место

.
Отсюда тотальное количество дефектных звонков равно

Вычисления вероятностей будем производить в соответствии с классическим определением вероятности.
I. Имея в виду, что

- вероятность того, что звонок будет обслужен

-ой станцией (доля звонков, обслуживаемых

-ой станцией)
и

- вероятность того, что обслуженный

-ой станцией звонок будет дефектным (доля дефектных звонков при обслуживании

-ой станцией),
согласно формуле Байеса, условная вероятность

вычисляется по формуле:


Получаем следующую формулу для вычисления условной вероятности

обслуживания дефектного звонка

-ой станцией:

II. Вероятность того, что дефектный звонок, случившийся на

-ой станции случился из-за события

на этой станции, вычисляется по формуле

так как

- общее количество дефектных звонков на

-ой станции, а
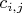
- количество дефектных звонков на этой станции по причине

.
III. Вероятность того, что во время обслуживания звонка

-ой станцией случится событие (авария)

, вычисляется по формуле

IV. Вероятность того, что любой звонок будет дефектным по причине события

на

-ой станции, вычисляется по формуле

V. Cогласно формуле Байеса, условная вероятность

- вероятность того, что случайно выбранный звонок оказался дефектным по причине

, вычисляется по формуле:

Здесь

- доля дефектных звонков из-за причины

,

- вероятность того, что звонок окажется дефектным, если произошло событие

.
Следовательно,

