Откуда Вы все это переписываете?
Первое из Кудрявцева.
Во втором модуль был, но я про него забыл.
Очень мило с Вашей стороны ))
Я криво изъясняюсь, простите, я имел ввиду то, что я не понимаю символы, которые в той формуле, а именно две стрелки.
-- 19.11.2014, 05:10 --В общем, насколько я понял, для того чтобы проверить необходимое условие равномерной сходимости на множестве

, мне нужно вычислить предел
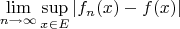
где

а где

- функция, к которой сходится ряд, то есть мне нужно ее явно выписать?
-- 19.11.2014, 05:18 -- -- 19.11.2014, 05:20 --
-- 19.11.2014, 05:20 --
