Вероятность.

[PeanoJr]

Здравствуйте!

В первом квадранте задана функция распределения системы двух случайных величин $F(x,y)=1+2^{-x}-2^{-y}+2^{-x-y}$.
Найти: а) двумерную плотность вероятности системы
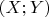
б) вероятность попадания случайной точки $(X;Y)$ в треугольник с вершинами $A(1;3), B(3;3), C(2;8)$

Вопрос по поводу пункта б. Можно ли найти искомую вероятность, достроив данный треугольник до прямоугольника, площадь которого в два раза больше, чем у треугольника, и затем разделить вероятность попадания в прямоугольник на два?

[Lia]

PeanoJr
Опечатка у Вас. Минус в правой части перед вторым слагаемым.

[PeanoJr]

Lia в сообщении #929951 писал(а):

PeanoJr
Опечатка у Вас. Минус в правой части перед вторым слагаемым.

Спасибо. Хотя прошу во всем винить Гмурмана :)
А пункт б) можно так, как я выше написал, решать?

[Lia]

Нельзя. Вам никто не обещал, что вероятности будут равными. Величина абсолютно непрерывна, ищите плотность, далее действуйте стандартно.

[PeanoJr]

Lia в сообщении #929953 писал(а):

Нельзя. Вам никто не обещал, что вероятности будут равными. Величина абсолютно непрерывна, ищите плотность, далее действуйте стандартно.

Значит, просто беру по области, заданной данным треугольником интеграл (от найденной плотности). Его удобно разбить на сумму двух: в качестве верхнего предела интегрирования $y$ будут уравнения прямых, на которых лежат стороны треугольника. Правильно?

[Lia]

При удачном выборе порядка интегрирования можно и одним обойтись.

[PeanoJr]

Lia в сообщении #929955 писал(а):

При удачном выборе порядка интегрирования можно и одним обойтись.

Да, я поторопился. Спасибо Вам!

[PeanoJr]

С ответом не сходится.
По функции распределения нашел плотность распределения: $\ln^{2}2\cdot2^{-x-y}$
Пределы интегрирования расставил следующим образом: $3\leqslant{y}\leqslant8$,
$\frac{y+2}{5}\leqslant{x}\leqslant\frac{18-y}{5}$
Получается: $\frac{135}{4096}$
Ответ в книжке: $\frac{5}{3\cdot2^{12}}$
В чем я ошибся?

[--mS--]

Да вроде ни в чём, у меня тоже получается $135/2^{12}$.