Добрый день,
Разбираю задачу по нахождению передаточной функции в электрической цепи. Если я правильно понял, то на схеме представлен колебательный контур
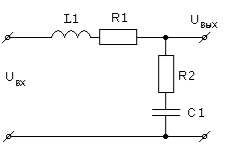
и передаточная функция для него, в соответствии с формулой для колебательного звеена в общем виде будет такой:

где

- коэффициент усиления или статический коэффициент передачи,

- постоянная времени и

- коэффициент затухания. Таким образом, применительно к данной схеме, формулы получат вид:



и, собственно, сама передаточная функция

Таким образом я выразил передаточную функцию через параметры элементов схемы (емкость, индуктивность и общее сопротивление), верно? А как представить, что такое статический коэффициент передачи

?

- это передаточная функция схемы при единичном импульсном воздействии

(функция Дирака)?