Неинтересно:

четно, а - - -
Не понял.
Я также не понимаю, зачем нужно, чтобы

было простым --- достаточно, чтобы

было нечётным. Допустим, что что

. Тогда порядок числа

по модулю

равен

. В частности,

делится на

. Значит, для некоторого нечётного простого делителя

числа

будем иметь

. Но тогда число

также делит

, при этом

является нечётным и

. Ясно, что

. Осталось заметить, что делимость
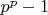
на

невозможна.