Э-э-э. У маленького треугольника неизвестно основание

, его надо найти, и высота

.

,

.
Спасибо за ответ! Но я не понимаю, откуда Вы получили

? Такое выражение получается путем подстановки

? Уж простите за глупый вопрос

Параметры

и

не являются независимыми, так как выбор точки

однозначно определяет положение точки

. Поэтому имеется ещё одно соотношение между

и

. Если уж Вы ввели систему координат, так напишите уравнения прямых

и

и найдите точку

.
Спасибо за ответ! Я так понимаю, координаты точки

нам как раз таки необходимы для нахождения

, в треугольнике

. То есть без рассмотрения подобия треугольников. Очень оригинально! Но и затруднительно одновременно.
Итак, получил уравнения прямых для

, для

. После решения равенства получил координаты:

Откуда мы узнаем

. Думаю дальше не имеет смысла продолжать. В принципе с самого начала это не имела смысла без координаты x_{0}; а зная ее нам бы не пришлось идти столь нерациональным путем. Поэтому, к сожалению, Ваш способ не подойдет.
Т.е. величина основания не зависит от положения т.

(доказывается через подобие треугольников, образованных наклонными прямыми). Поэтому т.

можно перенести на одну из сторон прямоугольника и рассмотреть треугольник, образованный с внешней стороны прямоугольника указанной стороной, продолжением основания и наклонной прямой, проходящей через т.

.
Вас понял. Иллюстрация
gris'а правильно трактует Ваши мысли? Если так, то это как минимум еще одна тропинка к ответу.
Кстати,
ответ должен получится
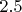
. Тут есть еще один вариант построения, но мне бы хотя бы на этот найти...