Ко́мпле́ксные числа — это упорядоченные пары действительных чисел
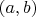
с определёнными на них операциями:

Видно, что числа вида

умножаются и складываются как вещественные. Это даёт основание отождествить их с вещественными и записывать просто как

.
Элемент

называют
мнимой единицей.

. Любое комплексное число
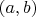
можно представить в виде

, а для укорочения записи вместо

пишут

.
(В приложениях — обычно когда буква

уже занята — используют вместо неё
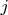
.)
Такая
алгебраическая форма записи 
позволяет выводить правила сложения и умножения, не запоминая их:

Примеры:

,

.
Внимание! Соотношение  нельзя читать как
нельзя читать как  («
(« — это корень из минус единицы»), и нельзя заменять в выкладках
— это корень из минус единицы»), и нельзя заменять в выкладках  на
на  !!!
!!!Первая компонента пары

называется
действительной частью комплексного числа и обозначается

, вторая —
мнимой частью комплексного числа,

, так что

Примеры:

,

,

,

.
Равенство

двух комплексных значений по определению эквивалентно двум равенствам

, так что, если известно

,

Сменив знак у мнимой части, получим
комплексно сопряжённое число

(альтернативное обозначение:

):

Можно установить следующие равенства:

Последнее выражение вещественно и неотрицательно, и мы вольны взять от него корень, получив
модуль, или
абсолютную величину, комплексного числа:

Если комплексное число

имеет только действительную компоненту

, его модуль совпадает с соответствующим модулем

действительного числа, отсюда и название.
Примеры:

,

,

.
ДелениеНа действительное число, как и умножать, делить просто:

.
Сопряжение подсказывает, как делить на комплексные числа. Надо найти

такой, что

. Умножим обе части на

:

.

, после этого поделим на действительное число

и получим

Заметим, что

.
Пример:

.
Заметка:

. Например,

и

; эти преобразования так же просто делаются и умножением на

.
Множество всех комплексных чисел

обозначается

и является полем.
(Полем?)
Поле — это множество

вместе с двумя бинарными операциями

и

(называемых «сложение» и «умножение» соответственно) на нём, для которых для всех элементов

выполняются следующие утверждения:
1.

(ассоциативность сложения).
2.

(коммутативность сложения).
3.

(существование нейтрального элемента для сложения).
4.

(существование обратного элемента по сложению).
5.

(ассоциативность умножения).
6.

(коммутативность умножения).
7.

(существование нейтрального элемента для умножения)
8.

(существование обратного элемента по умножению на

).
9.

(дистрибутивность

по

).
10.

(нетривиальность поля).
Примем как данность, что
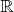
с обычными сложением и умножением является полем и покажем, как из этого следует, что

со сложением и умножением пар — тоже поле:
1, 2, 3 и 4 следуют из соответствующих свойств вещественного сложения, если выбрать нулём

и

.
5, 6 и 9 проверяются непосредственным вычислением.
7. Беря в качестве единицы

, получаем

.
8. В соответствии с соображениями о делении выше берём

, т. е.

получаем нужное.
10. Так как для поля
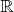
известно

,

.
Так как комплексные числа являются парами действительных, их можно рассматривать как точки некоторой плоскости (
комплексной плоскости) или радиус-векторы этих точек. Прямая, состоящая из действительных чисел

, зовётся
действительной осью. Прямая, состоящая из чисел вида

, называется
мнимой осью.
Операции принимают такое геометрическое истолкование:
•

— сумма векторов

и
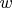
;
•

— вектор с тем же (

) или противоположным (

) направлением, что и

, но в

раз длиннее;
•

— проекции на вещественную и мнимую ось;
•

— отражение

относительно вещественной оси;
•

— длина вектора

;
•

— инверсия относительно единичной окружности

;
Чтобы разобраться с умножением, введём величину, которая вместе с модулем однозначно задаёт комплексное число —
аргумент. Аргумент

— это угол, на который нужно повернуть вокруг начала координат точку

, чтобы совместить её с

(таких углов, отличающихся на

, бесконечно много).

не определён.
•
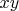
— это точка, получаемая из

поворотом на

и растяжением на

относительно начала координат.
Аргумент — многозначная функция. Порой бывает нужно выбрать одно значение из всех, называемое
главным значением аргумента и обозначаемое

. Как правило,

выбирается так, чтобы быть в промежутке
![$(-\pi;\pi]$ $(-\pi;\pi]$](https://dxdy-02.korotkov.co.uk/f/1/7/2/172c2b0fecdc03c281259dd70f83241882.png)
или

. Тогда любое ненулевое

однозначно сопоставляется паре

полярных координат

.
![\begin{tikzpicture}[scale=1.5,>=latex]
\draw[->](-0.5,0)--(1.8,0) node[above] {$\mathrm{Re}$};
\draw[->](0,-0.5)--(0,1.6) node[right] {$\mathrm{Im}$};
\fill (0,0) circle (0.04) node[below right] {$0$};
\draw[dashed, dash pattern = on 2 off 3] (0,0)--(1.06066017,1.06066017);
\draw[->] (0.6,0) arc (0:45:0.6);
\node[right] at (0.55,0.25) {\small$\arg z$}
\fill (1.06066017,1.06066017) circle (0.04) node[right] {$z$};
\node[left] at (0.65,0.75) {$|z|$};
\end{tikzpicture} \begin{tikzpicture}[scale=1.5,>=latex]
\draw[->](-0.5,0)--(1.8,0) node[above] {$\mathrm{Re}$};
\draw[->](0,-0.5)--(0,1.6) node[right] {$\mathrm{Im}$};
\fill (0,0) circle (0.04) node[below right] {$0$};
\draw[dashed, dash pattern = on 2 off 3] (0,0)--(1.06066017,1.06066017);
\draw[->] (0.6,0) arc (0:45:0.6);
\node[right] at (0.55,0.25) {\small$\arg z$}
\fill (1.06066017,1.06066017) circle (0.04) node[right] {$z$};
\node[left] at (0.65,0.75) {$|z|$};
\end{tikzpicture}](https://dxdy-02.korotkov.co.uk/f/d/5/c/d5c2719c535f8c46487f97467aa8ace182.png)
Аргумент и модуль комплексного числа
Пусть

и

. В соответствии с определением аргумента, синуса и косинуса получим:

Такое представление называют
тригонометрической формой комплексного числа.
Формула Эйлера и экспонентаЭкспоненту можно определить для любого комплексного числа

с помощью известного разложения в ряд

, сходящийся в каждой точке комплексной плоскости. При этом вещественная и мнимая часть ряда для

окажутся рядами для

и
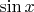
. Это приводит к
формуле Эйлера
и
экспоненциальной (показательной) форме записи комплексного числа

более короткой, чем тригонометрическая.
Пример:

.
По аналогии с вещественным случаем,

часто обозначается как

, но не стоит понимать такую запись как возведение числа

в комплексную степень.
Утверждения

по-прежнему верны, что даёт выражение комплексной экспоненты через функции вещественного аргумента:

Оба множителя не обращаются в ноль ни в одной точке, так что

.
В показательной форме умножение и деление благодаря свойствам экспоненты принимают такой вид:

что объясняет данную выше геометрическую интерпретацию умножения.
Заметьте, что

, так что

, то есть, экспонента имеет период

.
ЛогарифмНа комплексных числах также существует и натуральный логарифм, обратная к экспоненте функция. Из-за периодичности последней логарифм — многозначная функция:

Каждый способ выбора главного значения аргумента определяет главное значение логарифма, однозначную функцию

.
Как

, так и

не определены. Для ненулевых же

выполняется

, а вот

.
Из свойств экспоненты получаем
 Степени и корни
Степени и корниСтепень с целочисленным показателем определяется так же, как и в случае вещественных чисел:

В показательной форме возведение в степень выглядит так:

Она распространяется и на

.
Определим теперь корень целочисленной степени
![$\sqrt[n]w$ $\sqrt[n]w$](https://dxdy-04.korotkov.co.uk/f/f/b/9/fb9c756c4d0a00e0de737608b8d8d8cf82.png)
, решив уравнение

:
![$$r^ne^{in\varphi} = |w|e^{i\operatorname{Arg}w} \Leftrightarrow$$$$\Leftrightarrow r^n = |w| \mathbin\text{и} n\varphi = \arg w + 2\pi k \Leftrightarrow$$$$\Leftrightarrow r = \sqrt[n]{|w|} \mathbin\text{и} \varphi = \frac{\arg w}n + \frac{2\pi k}n,$$ $$r^ne^{in\varphi} = |w|e^{i\operatorname{Arg}w} \Leftrightarrow$$$$\Leftrightarrow r^n = |w| \mathbin\text{и} n\varphi = \arg w + 2\pi k \Leftrightarrow$$$$\Leftrightarrow r = \sqrt[n]{|w|} \mathbin\text{и} \varphi = \frac{\arg w}n + \frac{2\pi k}n,$$](https://dxdy-02.korotkov.co.uk/f/9/8/a/98a2a150ebb36779263b3d109ec79ed982.png)
где

, что отвечает

комплексным числам
![$z_k = \sqrt[n]{|w|}e^{\frac{\arg w}n + \frac{2\pi k}n}, 0\leqslant k<n$ $z_k = \sqrt[n]{|w|}e^{\frac{\arg w}n + \frac{2\pi k}n}, 0\leqslant k<n$](https://dxdy-03.korotkov.co.uk/f/2/3/5/235f4eb427f943ffeee0408c2f62a59182.png)
.
Корень

-й степени, как и аргумент — многозначная функция.
Например,

имеет два значения:

. Предостережение в начале связано с тем, что, обозначая как

только одно из значений, можно путём неаккуратных преобразований, навеянных свойствами действительных чисел, прийти к противоречию.
![\begin{tikzpicture}[scale=1.5,>=latex]
\draw[->](-1.9,0)--(2.2,0) node[above] {$\mathrm{Re}$};
\draw[->](0,-1.9)--(0,2.6) node[right] {$\mathrm{Im}$};
\fill (0,0) circle (0.04) node[below right] {$0$};
\draw[dotted] (0,0) circle (1.5);
\draw[dashed, dash pattern = on 2 off 3] (0,0)--(-0.9994358328285693,2.4128515423363814);
\draw[dashed, dash pattern = on 2 off 3] (0,0)--(1.38581929876693,0.5740251485476346);
\draw (0.4,0) arc (0:112:0.4);
\draw (0.6,0) arc (0:22:0.6);
\node[above] at (0.22222809320784093,0.3325878449210181) {\small$\varphi$}
\node[right] at (0.5884711682419382,0.15) {\small$\varphi/5$}
\fill (1.3058258449441862, 0) circle (0.04) node[below] {$1$};
\fill (-0.9994358328285693,2.4128515423363814) circle (0.04) node[left] {$z$};
\fill (1.38581929876693,0.5740251485476346) circle (0.04) node[right] {$w_1$};
\fill (-0.11768864359176731,1.495376000599692) circle (0.04) node[above left] {$w_2$};
\fill (-1.4585548805965147,0.3501680457838583) circle (0.04) node[left] {$w_3$};
\fill (-0.7837478470739229,-1.2789602465311387) circle (0.04) node[below left] {$w_4$};
\fill (0.9741720724952758,-1.1406089484000463) circle (0.04) node[below right] {$w_5$};
\end{tikzpicture} \begin{tikzpicture}[scale=1.5,>=latex]
\draw[->](-1.9,0)--(2.2,0) node[above] {$\mathrm{Re}$};
\draw[->](0,-1.9)--(0,2.6) node[right] {$\mathrm{Im}$};
\fill (0,0) circle (0.04) node[below right] {$0$};
\draw[dotted] (0,0) circle (1.5);
\draw[dashed, dash pattern = on 2 off 3] (0,0)--(-0.9994358328285693,2.4128515423363814);
\draw[dashed, dash pattern = on 2 off 3] (0,0)--(1.38581929876693,0.5740251485476346);
\draw (0.4,0) arc (0:112:0.4);
\draw (0.6,0) arc (0:22:0.6);
\node[above] at (0.22222809320784093,0.3325878449210181) {\small$\varphi$}
\node[right] at (0.5884711682419382,0.15) {\small$\varphi/5$}
\fill (1.3058258449441862, 0) circle (0.04) node[below] {$1$};
\fill (-0.9994358328285693,2.4128515423363814) circle (0.04) node[left] {$z$};
\fill (1.38581929876693,0.5740251485476346) circle (0.04) node[right] {$w_1$};
\fill (-0.11768864359176731,1.495376000599692) circle (0.04) node[above left] {$w_2$};
\fill (-1.4585548805965147,0.3501680457838583) circle (0.04) node[left] {$w_3$};
\fill (-0.7837478470739229,-1.2789602465311387) circle (0.04) node[below left] {$w_4$};
\fill (0.9741720724952758,-1.1406089484000463) circle (0.04) node[below right] {$w_5$};
\end{tikzpicture}](https://dxdy-01.korotkov.co.uk/f/0/b/2/0b27d8006c83e1588a2ce91e0e1d9e1682.png)
Корни 5-й степени
![$w_n = \sqrt[5]z$ $w_n = \sqrt[5]z$](https://dxdy-02.korotkov.co.uk/f/d/2/b/d2b11610a0f8afa57b1162282c51262882.png)
.
Корни

-й степени образуют вершины правильного

-угольника вокруг центра координат
![\begin{tikzpicture}[scale=1.5,>=latex]
\draw[->](-1.6,0)--(1.8,0) node[above] {$\mathrm{Re}$};
\draw[->](0,-1.5)--(0,1.6) node[right] {$\mathrm{Im}$};
\draw[dotted] (0,0) circle (1);
\fill (0,0) circle (0.04) node[above right] {$0$}
\fill (1,0) circle (0.04) node[above right] {$1$}
\fill (-1,0) circle (0.04) node[above left] {$-1$}
\fill (0,1) circle (0.04) node[above right] {$i$}
\fill (0,-1) circle (0.04) node[below right] {$-i$}
\end{tikzpicture} \begin{tikzpicture}[scale=1.5,>=latex]
\draw[->](-1.6,0)--(1.8,0) node[above] {$\mathrm{Re}$};
\draw[->](0,-1.5)--(0,1.6) node[right] {$\mathrm{Im}$};
\draw[dotted] (0,0) circle (1);
\fill (0,0) circle (0.04) node[above right] {$0$}
\fill (1,0) circle (0.04) node[above right] {$1$}
\fill (-1,0) circle (0.04) node[above left] {$-1$}
\fill (0,1) circle (0.04) node[above right] {$i$}
\fill (0,-1) circle (0.04) node[below right] {$-i$}
\end{tikzpicture}](https://dxdy-04.korotkov.co.uk/f/f/6/5/f65b69eb96410e2213b2c2c0171c8f4b82.png)
Корни четвёртой степени из единицы —

Возведение в комплексную степень

определяется как

.
Если в качестве
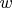
взять

или

, получатся определённые выше целочисленная степень или корень,
но возведение числа  в степень
в степень 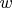 даст многозначную функцию
даст многозначную функцию  , а не
, а не 
.
Тригонометрические и гиперболические функцииИз формулы Эйлера следует

для

. Можно принять их определениями косинуса и синуса для любого комплексного аргумента подставляя вместо

комплексные числа. Определения гиперболических функций

распространяются на комплексные аргументы аналогично.
Пример. Благодаря такому определению, свойства тригонометрических функций типа формулы суммы углов или тождества

, верного и для

, можно вывести механически:

Функции

от комплексного аргумента выражаются через свои значения от вещественного так:

и связаны друг с другом так:

Равенства

продолжают работать и для

.
Обратные тригонометрические и гиперболические функцииВыразив тригонометрические и гиперболические функции через экспоненту, неудивительно прийти к выражению обратных через логарифм. Ниже приведены
многозначные функции.
 Основная (это название такое) теорема алгебры
Основная (это название такое) теорема алгебрыЛюбой многочлен с комплексными коэффициентами, не являющийся константой, имеет хотя бы один комплексный корень.
Следствие: уравнение

где

и

, в комплексных числах имеет ровно

корней с учётом их кратностей.
(Набросок доказательства.)
Многочлен

имеет корень

— иначе говоря, он представим как

. Многочлен

— либо константа, либо имеет корень

, и в любом случае имеет степень на одну меньше. Многочлен

-й степени, таким образом, распадётся в произведение

скобок

, т. е. будет иметь

корней с учётом их кратностей.
Иначе говоря, поле

алгебраически замкнуто.
Корни такого уравнения с вещественными

— вещественные числа и пары комплексно-сопряжённых. Пример:

.



