Задача:Даны плоскости:
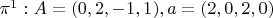
и

.
Через прямую

провести плоскость

, перпендикулярную плоскости

.
Если провести плоскость через прямую, направляющий вектор прямой будет входить в базис ЛПП плоскости.
Многомерные плоскости перпендикулярны, если перпендикулярны их линейные подпространства, то есть, как я понимаю, каждый вектор базиса одной плоскости, скалярно умноженный на каждый вектор другой плоскости, даёт нулевой вектор. Но тут

. Я что-то упускаю?