Определение параметра биномиального распределения

[Александрович]

Кролик в сообщении #838911 писал(а):

Позавчера ученик получил по контрольной 63 балла из 100 возможных. Вчера он получил по контрольной 87 баллов, а сегодня 74. Сколько баллов получит ученик на следующей контрольной, если считать, что качаство его знаний в предмете не прогрессирует и не регрессирует?

$n$ известно и равно 100. Чего вы тогда голову всем морочите?

[Кролик]

Александрович в сообщении #838912 писал(а):

$n$ известно и равно 100. Чего вы тогда голову всем морочите?

-- Параметр $n$ биномиального распределения, которое мы пытаемся положить в основу (неполной?) вероятностной модели не может быть равен 100. Ведь СКО тогда было бы меньше 5-ти. А уже из значений первых 3-х реализаций приведённого мной бытового примера видно, что разброс гораздо сильнее.

[Евгений Машеров]

Ваш пример на биномиальное распределение не похож совершенно. Либо это иное распределение, либо полученные значения статистическая флуктуация. И тогда аргумент, что "СКО было бы меньше 5" невалиден.

[Кролик]

Евгений Машеров в сообщении #838934 писал(а):

Ваш пример на биномиальное распределение не похож совершенно. Либо это иное распределение, либо полученные значения статистическая флуктуация. И тогда аргумент, что "СКО было бы меньше 5" невалиден.

-- Да, к сожалению, я ошибся в первом сообщении трэда, обозначив мощность области значений случайных величин и параметр биномиального распределения одной и той же буквой. Разумеется, что распределение $X_i$ не биномиальное, а иное, но нам не важно, какое оно в точности, т.к. полнота вероятностной модели не сама цель. Для моделирования достаточно, если область значений $X_i$ можно равномерно разбить на не очень большое число $n$ дизъюнктных интервалов, распределение попадания $X_i$ в которые близко к биномиальному. (Ну, в России ученикам ставят оценки от 1 до 5, а в Индии, например, более дифференцированно от 0 до 100.)

[Александрович]

Кролик в сообщении #838930 писал(а):

-- Параметр $n$ биномиального распределения, которое мы пытаемся положить в основу (неполной?) вероятностной модели не может быть равен 100. Ведь СКО тогда было бы меньше 5-ти. А уже из значений первых 3-х реализаций приведённого мной бытового примера видно, что разброс гораздо сильнее.

Да, действительно. $X_i$ меняется не от 0 до 100, а от $A$ до $B$ и $n=B-A$.

[Кролик]

Александрович в сообщении #838959 писал(а):

Да, действительно. $X_i$ меняется не от 0 до 100, а от $A$ до $B$ и $n=B-A$.

-- То есть, за пределами интервала $[A, B]\subset [0, 100]$ вероятность 0, а внутри этого интервала равномерное распределение? Разве это будет лучше описывать пегель успеваемости ученика?
Гипотез распределения может быть, действительно, несколько. Однако, у меня остаётся вопрос, как проверять их достоверность, если, скажем, $m\approx 7$?

[Александрович]

Я думаю распределение будет биномиальное с тремя параметрами $[X_{\min}; n; p]$. Как найти их выборочные оценки, знаете?

[Кролик]

Александрович в сообщении #839167 писал(а):

Я думаю распределение будет биномиальное с тремя параметрами $[X_{\min}; n; p]$. Как найти их выборочные оценки, знаете?

-- Причём теперь

$$ n \neq 100 - X_{\min}\, ,\qquad (2) $$

Вы согласны?
Как уже обсуждалось выше, важны не только формулы статистической аппроксимации параметров, но и оценки качества получающихся аппроксимаций. Евгений Машеров предложил выше простой и изящный способ получения обоих параметров биномиального распределения вместе с оценками их достоверности в случае, если не (2) имеет силу. Однако, поскольку (2) на самом деле в силе, то нужна всё-таки агрегация по подинтревалам. Некий фильтр $X_i -\!\!\!\!> Y_i$, где от $Y_i$ уже, действительно, можно ожидать биномиальности с параметрами $[Y_{\min}; n; p]$.
Т.о. на Ваш последнй вопрос ответ остаётся отрицательный, поскольку (2) увы..

[Александрович]

Евгений Машеров в сообщении #838934 писал(а):

Ваш пример на биномиальное распределение не похож совершенно.

Да, совершенно с вами согласен. И $X_{\min}$ можно не рассматривать.

[Александрович]

Кролик в сообщении #839213 писал(а):

Евгений Машеров предложил выше простой и изящный способ получения обоих параметров биномиального распределения вместе с оценками их достоверности в случае, если не (2) имеет силу.

Это где такое было?

[Александрович]

Кролик в сообщении #838911 писал(а):

Позавчера ученик получил по контрольной 63 балла из 100 возможных. Вчера он получил по контрольной 87 баллов...

Из позавчерашней выборки 95%-ный интервал для генерального среднего [50,8;75,2].
Из вчерашней выборки - [79,8;94,2].
Интервалы не пересекаются, следовательно выборки не однородные, то есть не принадлежат к одному распределению.

[Кролик]

Александрович в сообщении #839542 писал(а):

Из позавчерашней выборки 95%-ный интервал для генерального среднего [50,8;75,2].
Из вчерашней выборки - [79,8;94,2].
Интервалы не пересекаются, следовательно выборки не однородные, то есть не принадлежат к одному распределению.

-- Это очень интересно. Большое спасибо. Не могли бы Вы посчитать теперь те же интервалы для той же задачи, но с другими цифрами?

Позавчера ученик получил по контрольной 13 баллов из 20 возможных. Вчера он получил по контрольной 17 баллов, а сегодня 15. Сколько баллов получит ученик на следующей контрольной, если считать, что качаство его знаний в предмете не прогрессирует и не регрессирует?

-- Вс мар 23, 2014 10:39:04 --

Мысли Машерова см. в сообщении post838869.html#p838869.

[Кролик]

Александрович в сообщении #839167 писал(а):

Я думаю распределение будет биномиальное с тремя параметрами $[X_{\min}; n; p]$. Как найти их выборочные оценки, знаете?

— Подытожив все предложенные идеи, я выписал следующую модель аппроксимации небиномиальной случайной величины $X \in \{0, 1, ..., 100\}$ биномиальной $Y \in \{0, 1, ..., n\}$. Пусть область допустимых значений $[x_{\min}, 100]$ дизъюнктно разбита на $n < 100$ равных интервалов, порождающих статистические классы с частотами $h_i$ и средними $\bar y_i$. Формулы аппроксимации матожидания и дисперсии тогда будут следующие:

$$ \bar y &=& \frac{1}{m} \sum_{j=1}^{m} y_j\, , \qquad s^2 &=& \frac{1}{m-1} \sum_{i\,\in I} h_i\, (\bar y_i - \bar y) \eqno(3) $$

где введены такие обозначения

$$ I=\{ i\in \{0, 1, ..., n\}: J_i\neq\emptyset\}\, ,\quad J_i=\{ j\in \{0, 1, ..., m\}: i-1 < y_j \le i \}\quad\eqno(4)$$ $$\bar y_i = \frac{1}{h_i}\sum_{j\in J_i} y_j\quad i\in I\, ,\quad\mbox{где}\quad h_i=|J_i|\quad\mbox{и}\quad y_j = n\;\frac{x_j - x_{\min}}{100 - x_{\min}}\eqno(5)$$

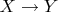
Предположим, что при некоторых параметрах $x_{\min}$ и $n$ определённое выше отображение $X\to Y$ порождает новую случайную величину, близкую к биномиальной. Тогда логично предположить, что пара нижестоящих переменных хорошо приближает матожидание и дисперсию биномиального распределения в следующем смысле:

$$ M = \bar y / n \approx p\quad\mbox{}\quad S=s/\sqrt{n}\approx q =\sqrt{p(1-p)}\eqno(6) $$

Определим теперь аппроксимацию $p^*$ не по формуле Otta $(1)$ (см. вервый ответ в трэде), а в силу решения следующей экстремальной задачи с невыпуклым ограничением:

$$ \Phi_n(p, q) = (p-M)^2 + (q-S)^2 \to \min_{0\le p, q\le1}\eqno(7) $$$$ \mbox{s.t.}\quad q^2 + (p-1/2)^2 = (1/2)^2\eqno(8) $$

аналитическое решение которой в данном случае нетрудно найти:

$$ p^*=\frac{1}{2}\left[\frac{(M-1/2)}{Q}+1\right]\, ,\quad \Phi_n^*= \frac{1}{4}\left(1-2Q\right)^2\, , \eqno(9) $$$$\quad\mbox{где}\quad Q=\sqrt{(M-1/2)^2 +S^2}\, . $$

Причём в формулах $(9)$ параметры $x_{\min}, n < 100$ подобраны так, что они доставляют глобальный минимум функции $\Phi_n^*$. Получив описанным образом оптимальные параметры $x_{\min}^*$ и $n^*$, можно вычислить доверительный интервал для $p^*$ по опубликованным уже на форуме формулам Александровича.
Остаются ли ньюансы?