Есть интеграл, который я не могу решить:

Существует универсальная тригонометрическая подстановка, но поскольку мы проходили её "условно", то предполагается, что использовать её не нужно для решения этого примера.
Мне сказали, что первым действием необходимо перейти к половинному аргументы, заменив

на
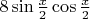
,

на

И разложив единицу по основному тождеству (с тем же половинным аргументом, разумеется).
Вопрос в том, что делать дальше?
Выражение, которое у меня получается после приведения всего не слишком красивое, сходу разложить его как-то не удаётся.