Принесли три хороших вектора
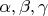
, на которых можно построить треугольник. Положили их на стол. Вася дождался, когда все выйдут из комнаты, и изменил знак вектора

, однако на этикетке так и осталось просто

, так что потом все думали, что это исходный вид вектора. Но понятно же, что всё равно его можно использовать с двумя другими векторами для построения треугольника. Просто процедура проверки должна быть чуть сложнее и учитывать возможность таких модификаций знака, которые, в общем, ничему не мешают. Как изменить проверку?
provincialka намекала.