Здравствуйте, дорогие друзья!
Пусть

Как связан

со знаком перестановки элементов множества

по правилу
 Моя попытка решения:
Моя попытка решения: Рассмотрим

в виде:

. Подействуем отображением

. Тогда получим:

Редуцируем по модулю

и получаем:

где

и

Так как

для

. Перемножая почленно сравнения эти получаем:

, но так как

и еще

. Тогда получаем, что:

где

- количество отрицательных среди
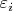
. Верно ли я решил? Или тут нужно что-то другое?