Продолжение последовательности чисел

, при которых существуют решения уравнения после

такое:

При

решение, например,

В качестве очередной задачи - можно найти решение уравнения при

.
P.S. Последовательность до определённых пределов легко продолжается.

включается в неё, если ранг кривой
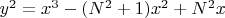
больше нуля.
Не знаю, есть ли эта последовательность в OEIS.