Обычно, если не отвечают, то заняты (на работе, или другие какие дела). Летом вообще народу на форуме меньше.
Несколько замечаний.
1) На контуре-источнике положительным направлением обхода лучше считать направление против часовой стрелки (если смотреть против оси

, т.е. сверху вниз). Оно же будет положительным направлением тока. Это направление вектора
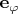
. Тогда для точки

элемент будет не

, а

. Проверка: для небольших положительных углов

должно быть

. Это легко увидеть на
Вашей картинке, если принять, что наблюдатель находится в плоскости

. Тогда

направлена к нам (вернее, "под нас"), а

слева направо. Направление вектора

такое же, как
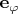
.
2) Можно сейчас забыть о втором контуре, а рассматривать только один контур-источник и точку

, где рассматривается поле. Поэтому вместо

можно писать

.
3) Самое страшное и ужасное. Точку

надо брать не радиально противоположную точке

, а симметричную ей относительно плоскости

, проходящей через

и

. В данном случае

— это плоскость

. Поэтому координаты точки

будут

. Соответствующий элемент кольца, тоже зеркально симметричный относительно

, будет

. Итак:


4) В формулах для

не нужно писать модуль в правой части. Векторное произведение даёт вектор, и это правильно, так как слева тоже вектор. Но модулем мы превращаем вектор в скаляр, получается, что вектор слева равен скаляру справа. Надо так:
![$d\mathbf B=k\frac{[d\mathbf l, \mathbf r]}{r^3}$ $d\mathbf B=k\frac{[d\mathbf l, \mathbf r]}{r^3}$](https://dxdy-02.korotkov.co.uk/f/5/7/e/57e5844acedf2d0cc452bc7c63e8437c82.png)
Собственно вывод. Нам надо доказать, что

лежит в плоскости

, или, что эквивалентно, его

-компонента равна нулю. Сразу заметим, что

(этого бы не было, если бы точка

бралась диаметрально противоположной

). То есть

(но не

!) для обоих элементов общее, поэтому общий множитель

можно вынести за скобки и забыть о нём.
Остаётся доказать, что
![$[d\mathbf l_A, \mathbf r_A]+[d\mathbf l_B, \mathbf r_B]=[d\mathbf l_A, \vec{AC}]+[d\mathbf l_B, \vec{BC}]$ $[d\mathbf l_A, \mathbf r_A]+[d\mathbf l_B, \mathbf r_B]=[d\mathbf l_A, \vec{AC}]+[d\mathbf l_B, \vec{BC}]$](https://dxdy-04.korotkov.co.uk/f/f/a/6/fa6fc824847d112d2c4fd0293ec2a0d182.png)
обладает нужным свойством.
Подсказка: удобно заменить


При правильном подходе даже не нужны явные выражения для координат точек и элементов, полученные ранее.



